高一下同步练习卷任意角的三角函数
4．3
A组
1．已知角a 终边上一点P 的坐标为（2＋
，2－），求这个角的六个三角函数值．
2．作出下列各角的正弦线、余弦线、正切线：
（1）70°； （2）－110°； （3）
； （4）
．
3．给出下列命题：
（1）正角的三角函数值是正的，负角的三角函数值是负的；
（2）设P（x，y）是角a 终边上的一点，因为sina ＝
，所以a 的正弦值与点P的纵坐标y成正比；
（3）若sinq·cosq ＞0，则q 一定在第一象限；
（4）两个角的差是2p 的整数倍，则这两个角的同一个三角函数的值必相等；
（5）若角a 的终边落在y轴上，则角a 的正弦线是单位长度的有向线段．其中正确命题的序号是________．（将正确的都写出来）
4．确定下列各三角函数值的符号：
（1）sin182°； （2）cos（－43°）； （3）tan
；
（4）sin980°； （5）cos
； （6）tan
．
5．求满足下列条件的角x的范围：
（1）sinx·tanx＜0； （2）｜－cosx｜＝－cosx．
6．如果角
的始边与x轴正半轴重合，顶点与原点O重合，角的终边上有一点P，OP＝2，那么P点的坐标为（ ）．
A．（1，－
） B．（－1，） C．（－，1） D．（－，－1）
7．a 是第二象限角，其终边上一点为P（x ，），且cosa ＝
x，则sina 的值为（ ）．
A．
x
B．
C．
D．－
8．求下列各式的值：
（1）
；
（2）
．
9．已知f（x）＝sinx＋3cosx－2tan2x，则f（
）＝________；f（
）＝________；f（
）＝________．
10．求证：
（1）角q 为第三象限角的充分必要条件是sinq ＜0且tanq ＞0；
（2）角q 为第二或第四象限角的充分必要条件是sinq ·cosq ＜0．
11．求下列三角函数值：
（1）sin780°； （2）
； （3）cos（－675°）； （4）
；
（2）tan6p ； （6）
； （7）
； （8）
；
B组
1．下列对三角函数线的描述正确的是（ ）．
A．只有象限角，才存在三角函数线
B．若a 为第一象限角且sina 用MP表示，则p＋a 的正弦应该用PM表示
C．用有向线段表示三角函数值，线段越长，则相应的三角函数值越大
D．当角a 终边落在y轴上时，正切线不存在
2．作出下列各角的正弦线、余弦线、正切线：
（1）
；
（2）
； （3）
．
3．确定下列三角函数值的符号：
（1）sin182°3′； （2）sin（－4896°）； （3）
；
（4）
（5）sin1； （6）cos2．
4．判定下列各式的值是正还是负：
（1）cos40°－cos140°； （2）
； （3）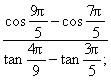
（4）cos2－sin2；
（5）
．
5．求下列三角函数值：
（1）cos720°；
（2）
； （3）
（4）
； （5）sin（－1071°）； （6）tan1865°．
6．在直角坐标系中，角a 的终边过点P（－3a，4a）（a≠0），则sina ＝________．
7．设a 为第一象限角，那么在sin2a 、cos2a 、tan2a 、
、
、
中一定取正值的有（ ）．
A．1个 B．2个 C．3个 D．4个
8．由下列条件决定的q 角中，一定是第二象限角的是（ ）．
A．sinq·cosq ＜0 B．sinq ≥0且cosq ＜0
C．2q 是第四象限角
D．
9．化简求值
．
10．设
是角
的终边上的点，按下列条件求cos．
（1）
；（2）
．
11．设a ＝
，b ＝
，求下列各式的值：
（1）
；
（2）
．
12．已知x、y都是实数，且
，求
的值．
拓展练习
1．若角a 的终边经过直线2x－3y－7＝0和直线3x＋2y－4＝0的交点，则tana ＝________．
2．已知a 、b 均为第二象限角，且sina＞sinb，则（ ）．
A．tana ＞tanb B．cosa ＜cosb C．cosa＞cosb D．a ＞b
3．已知sina ＞sinb ，那么下列命题成立的是（ ）．
A．若a 、b 是第一象限角，则cosa ＞cosb
B．若a 、b 是第二象限角，则tana ＞tanb
C．若a 、b 是第三象限角，则cosa ＞cosb
D．若a 、b 是第四象限角，则tana ＞tanb
4．已知角a 的顶点在原点，始边与x轴正半轴重合，终边为射线4x＋3y＝0（x≥0），求5sina －3 tana＋2cosa的值．
5．二次函数y＝f（x）当x分别取0、、p 时，它的函数值与sinx的相应值相同，求此二次函数．
参考答案
A组
1．由
，
，得
∴ 
，
，
，cota ＝－9－
，
，
.
2．（1）
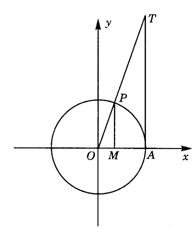
有向线段MP为70°角的正弦线
有向线段OM为70°角的余弦线
有向线段AT为70°角的正切线
（2）
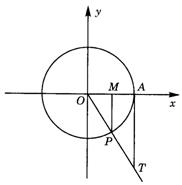
有向线段MP为－110°角的正弦线
有向线段OM为－110°角的余弦线
有向线段AT为－110°角的正切线
（3）
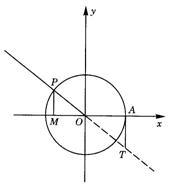
有向线段MP为
角的正弦线
有向线段OM为角的余弦线
有向线段AT为角的正切线
（4）
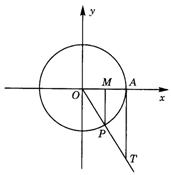
有向线段MP为角的正弦线
有向线段OM为角的余弦线
有向线段AT为角的正切线
图答4－3
3．（4），（5）
4．（1）－；（2）+；（3）－；（4）－；（5）－；（6）＋．
5．（1）
，k∈Z；
（2）
，k∈Z．
6．B．P点横坐标
，纵坐标
。
7．A．注意x＜0，可得
．
8．（1）（P－1）2；（2）
．
9．
；
，
．
10．（1）充分性：若sinq ＜0，则q 的终边位于第三或第四象限．也有可能在y轴负半轴上，又tanq ＞0，则q 角终边位于第一或第三象限，而sinq ＜0，tanq ＞0同时成立，则角q 终边位于第三象限，故角q 为第三角限角，必要性略．
（2）充分性：若sinq·cosq ＜0，则可能sinq ＞0且cosq ＜0，此时q 角终边第二象限，也有可能sinq ＜0且cosq ＞0，此时角q 终边位于第四象限，故q 角为第二或第四象限角.
11．（1）
；（2）
；（3）
；（4）；（5）0；（6）0；（7）
；（8）－1．
B组
1．D．
2．
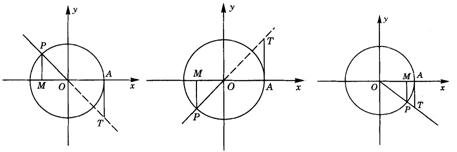
图答4－4
以上三图中有向线段MP为正弦线，有向线段OM为余弦线，有向线段AT为正切线
3．（1）－；（2）＋；（3）＋；（4）＋；（5）＋；（6）－．
4．（1）＞0；（2）＜0；（3）＞0；（4）＜0；（5）＞0．
5．（1）1；（2）；（3）；（4）0；（5）0.1564；（6）2.1445．
6．当a＞0时，
，当a＜0时，
．
7．B．一定取正值的是sin2a，．
8．D．由等式化简可知sinq ＞0且tanq ＜0．即q 为第二象限角．
9．当q 为第一象限角时，原式＝3；当q 为第二象限角时，原式＝－1；当q 为第三象限角时，原式＝－1；当q 为第四象限角时，原式＝－1．
10．（1）由定义得
，解得，
．
（2）由定义得
，解得x＝1，
．
11．（1）1；（2）－8．
12．由条件可得x＝6且y＝－2，代入求得原式＝1．
拓展练习
1．由
求得
则
．
2．C．利用三角函数线比较．
3．D．利用单位圆三角函数线．
4．先选一个特殊点（3，－4），可分别求得，
，
，从而求得
．
5．设
（a≠0），f（0）＝c＝sin0＝0（1），
（2）
（3），由（1）（2）（3）解得
，
，c＝0
∴ 
.