高一下学期期末考试数学试题
第I卷
一．选择题：（每题5分，共60分，只有一选项符合题目要求）
1.若角a的终边过点P（0，m）、（m≠0）则下列各式中无意义的是（ ）
（A）sina (B)cosa (C)tana (D)csca
2.若向量
=(1,1) 
=(1,-1) 
=(-1,2)则等于（ ）
3.向量=(n,1) =(4,n)共线且方向相同，则n等于( )
4.下列函数中既是奇函数，又是以π为最小正周期的函数是（ ）
（A）y=tan 2x (B)y=
(C) y=sin(
) (D)y=cos(
)
5.已知命题p:
与
共线，命题q:有且只有一个实数
,使
则命题p是命题q的( )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分又不必要条件
6.正方形ABCD三个顶点坐标分别为（0，-1） （4，1）和（2，5），则第四个顶点坐标为（ ）
(A) (-2,3) (B)(-1，2,) (C)(-3,2) (D) (-2,1)
7.
ABC中，已知a=5
，c=10 , A=
则B等于（ ）
(A) 
(B)
(C)
(D) 或
8．已知
， 
则与的夹角是( )
(A)
(B) (C) (D)
9.若O是ABC内一点且
则O是ABC的( )
(A)内心 (B)外心 (C)垂心 (D)重心
10.
的值在区间为（ ）
(A)(43,44] (B)(44,45] (C)(45,46] (D)(46，47]
11.已知sinQ=-
且Q
,则Q可表示为（ ）
(A)arcsin (B)
(C)
(D) 
12．若把直角三角形的三边各增加一个单位，则所得的三角形为（ ）
(A)锐角三角形 (B)直角三角形 (C)钝角三角形 (D)不能确定
二．填空题：（每题4分 共16分）
13．已知
为第一象限角，则sin 2, cos 2 tan2, ,sin
,
tan
中必定为正值的有
14．已知A(3,-2) B(cosa-2,sina+3) 则
的最大值为
15. 已知向量
=(2,-4)及表示该向量的有向线段的始点A(5,1),则它的终点B的坐标是
16.下列命题中
①若
,则= ②零向量与任一向量都平行
③若
,则
④设
是平面
内所有向量的一组基底，若实数
使
,则
;
其中正确的命题序号为
三．解答题：（共74分）
17．一个函数的图象按
平移后得到的图象的函数解析式为
，求原来函数的解析式。（10分）
18．已知
. 
， 求
的值。（12分
19．点O(0,0) A(2,0) B(-2,0)为直角坐标平面内的三个点，点P满足下列两个条件(1)3
(2)
，求点P的坐标及
的值。
(12分)
20.已知A(-2，10) B(1，6) C(x,2)且三点共线，O为坐标原点，求向量
的夹角的余弦值。(13分)
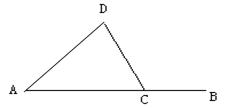
21.如图甲船自A港沿东偏北方向向外行驶，乙船在离A港正东7海里B处驶回该港，甲乙两船航速之比2:1
求两船距离最近时各离A港多远?
(13分)
22.已知向量
和向量
的对应关系可用
表示 (14分)
（1）向量
,求向量
的坐标
（2）求使
的向量
的坐标
（3）求证对任意向量
及常数m,n恒有
成立
下学期期末考试高一数学答案
一．CCCDBADCDCDA
二．13 sin2 tan
,
14 5+1
15(7,-3), 16 ②④
三．
17解：设（x,y）在原来函数上，（
）在
上 则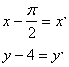 
代入 的原来函数的解析式为
18解：∵ cos(
)=-1
∴=2kπ+π
(k
z)
2=2kπ+π+ (kz)
∴sin(2)=sin(2kπ+π+)
=sin(π+)=-sin=-
19解：设P(x,y)则
=(x-2,y)
=(x+2,y)
∵3 既 3
得
x
-5x+4=0 ①
又∵·=0 得 x=4代入①式得
x=
y=
∴P(,) =2
20解：∵点A B C三点共线
∴点C分有向线段AB的比
∴
x=4 
=（1，6）
=（4，2）
设Q为向量的夹角
则 cosQ=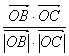
=
21解：设乙船航行的距离为x海里，则甲船航行的距离为2x海里,既AD=2x, AC=7-x
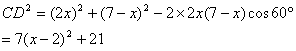
∴x=2时，CD有最小值
，此时AD=4，AC=5
∴两船距离最近时，甲船离港4海里，乙船离港5海里
22解：(1)∵ 既f(
)=(y,2y-x)
∴f()=(1,2×1-1)=(1,1)
同理f()=(0,-1)
(2)设=（m,n） 则f()=(n,2n-m)=(p,q)
∴n=p 2n-m=q得m=2p-q
∴=(2p-q,p)
(3)设=(i,j) =(s,t)则
f()=(j,2j-i) f()=(t,2t-s)
mf()+nf()=(mj+nt,2jm-im+2tn-sn)
=(mj+nt,2(mj+nt)-(mi+ns))
=f(m+n)
∴对任意向量及常数m,n恒有成立