| 函数y＝Asin(ωχ+φ)的图象 |
一、填空题
1．要得到
的图象，只要将
的图象向 平移 个单位。
2．已知函数
，若图象上每一点的纵坐标保持不变，横坐标伸长到原来的2倍，然后将所得图象沿
轴向右平移
个单位，恰好得函数的图象
，则的表达式为 。
3．函数
的振幅为 ，周期为
，相位为 ，初相为 。
4．（1）将函数
的图象向左平移
个单位，所得到的函数图象的解析式为： ；
（2）将函数
的图象向右平移1个单位后，所得到的函数图象的解析式为：
。
5．已知函数
的最大值是
，最小值是－
，则函数
的最小正周期是 。
二、解答题
1．画出下列各函数在一个周期长度上的图象（视为由
，
的图象作变换而得的那一个周期且取1 crn表示五个单位取
建立坐标系用“五点法”作图）
（1）
； （2）
；
（3）
； （4）
2．由曲线
的主要特征写出其解析式（其中
，
）：
（1）在
时，
最大为2，从点（
，2）向右逐渐下降第一次交轴于
；
（2）过（，0）点，自该点向右逐渐升至（
，3）后又逐渐下降；
（3）相邻的两条对称轴是直线
和
，且过点（
，2）；
（4）直线是一条对称轴，且这条对称右边最近的一个对称中心的坐标是
（
，0），在
内图象逐渐下降，过点（
，5）
提示：如不能根据文字描述想象出图象的形状，要画出草图，然后再求A。
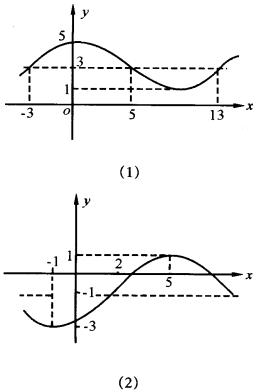
3．已知函数
的图象如图（1）、（2），分别求出它们的解析式。
4．已知曲线的一个对称中心坐标为（6，3），且距点（6，3）最近的一个最高点的坐标为（1，5），求：
（1）函数的解析式；
（2）函数的最大值和最小值及取得最大、最小值的值的集合；
（3）曲线的对称轴方程和对称中心的坐标．
5．求下列各振动曲线
的振幅，周期、频率、相位和初相；
（1）
；
（2）
；
（3）
；
（4）
【参考答案】
一、填空题
1．右； 2．
3．
；
；
；－
4．（1）
（2） 
5．
二、解答题
1．
2．（1）由已知
，故
，又
，且与（，0）关于直线的对称点为（0，0），所以
；
（2）由已知，
，
，故
，又从点（，0）向右逐渐上升，所以，
；
（3）由已知，，
，故
，又点（
，0）是对称中点，
也是对称中点，且自点
向右逐渐上升，所以
（4）由已知，
，故，且也是对称中心，自向右逐渐上升，所以
。
3．（1）
；（2）
4．（1）由已知，
，故
，
又
，与点（6，3）关于直线
对称点为（－4，0），且从点（－4，0）曲线逐渐上升，所以：
，
即
；
（2）由
，
由
∴ 最大为5，取得最大值的的集合为
，
最小为1，取得最小值的的集合为
（3）由
，
由
∴ 对称轴方程为
，
。
对称中心坐标为（
，3），
5．（1）振幅为2，周期
，频率
，相位是
，初相是；
（2）振幅为3，周期为
，频率
，相位是
，初相是
；
（3）振幅是5，周期
，频率
，相位是
，初相是2；
（4）振幅是4，周期
，频率
，相位是
，初相是。