函数综合题

高一（上）数学单元同步练习

函数综合题

一、 选择题

1、函数的定义域为A，函数的定义域为B，则

（A）　　（B）　 （C）　 （D）

2．已知P>q>1,0<a<1,则下列各式中正确的是（　 ）

（A）a⁰>a^q（B）P^a>q^a （C）a^-p<a^-q （D）p^-a>q^-a

3.若-1<x<0，那么下列各不等式成立的是（　 ）

（A）2^-x<2^x<0.2^x  （B）2^x<0.2^x<2^-x

（C）0.2^x<2^-x<2^x  （D）2^x<2^-x<0.2^x

4.函数y=(a²-1)^-x与它的反函数在（0，+）上都是增函数，则a的取值范围是（　 ）

（A）1<<　　  （B）<且

（C）>　　　　（D）>1

5．函数y=log_ax当x>2 时恒有>1，则a的取值范围是（　）

（A）　　　 （B）0

（C）　　　　　　　 （D）

6．函数y=log_a²(x²-2x-3)当x<-1时为增函数，则a的取值范围是（　 ）

（A）a>1　（B）-1<a<1　 （C）-1<a<1且a0　（D）a>1或a<-1

7．函数f(x)的图像与函数g(x)=()^x的图像关于直线y=x对称，则f(2x-x²)的单调减区间为（　）

（A）（0，1）　 （B）[1，+）　 （C）（-，1］　（D）[1，2）

8．设函数f(x)对xR都满足f(3+x)=f(3-x),且方程f(x)=0恰有6个不同的实数根，则这6个实根的和为（　 ）

（A）0　　（B）9　　（C）12　 （D）18

9．已知f(x)=logx,则不等式[f(x)]²>f(x²)的解集为（　 ）

（A）（0，）　　　　  （B）（1，+）

（C）（，1）　　　　  （D）（0，）（1，+）

10．函数f(x)=log_a,在（-1，0）上有f(x)>0，那么（　　）

（A）f(x)(- ,0)上是增函数　　　　　 （B）f(x)在（-，0）上是减函数

（C）f(x)在（-，-1）上是增函数　　　（D）f(x)在（-，-1）上是减函数

11、函数的定义域为A，函数的定义域为B，则

（A） （B）　 （C）　 （D）

12．.函数f(x)=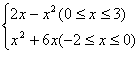的值域是（　 ）

（A）R　　 （B）[-9，+）　 （C）[-8，1]　 （D）[-9，1]

13．如果函数y=x²+ax-1在区间[0，3]上有最小值-2，那么a的值是（　 ）

（A）2　 （B）-　 （C）-2　 （D）2或-

14．函数y=x²-3x(x<1)的反函数是（　 ）

（A）y=(x>-)　　　　 （B）y=(x>-)

（C）y=(x>-2)　　　　 （D）y=(x>-2)

15．若U=R，A=B=，要使式子AB=成立，则a的取值范围是（　 ）

(A)-6　　　　　　  (B)-11<

(C)a　　　　　 (D)-11

16．某厂1988年的产值为a万元，预计产值每年以n%递增，则该厂到2000年的产值（单位：万元）是（　 ）

（A）a(1+n%)¹³  （B）a(1+n%)¹²

（C）a(1+n%)¹¹  （D）

17．已知A、B两地相距150千米，某人开汽车以60千米/小时的速度从A地到达B地，在B地停留1小时后再以50千米/小时的速度返回A地，把汽车离开A地的距离x表示为时间t（小时）的函数表达式是（　 ）

（A）x=60t　　　　　 （B）x=60t+50t

（C）x=　　　　（D）x=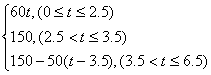

18．某工厂第三年的产量比第一年的产量增长44%，若每年的平均增长率相同（设为x），则以下结论正确的是（　　）

（A）x>22%　　　　　　　　　　  （B）x<22%

（C）x=22%　　　　　　　　　　  （D）x的大小由第一年的产量确定

19．由于电子技术的飞速发展，计算机的成本不断降低，若每隔5年计算机的价格降低，现在价格8100元的计算机15年后的价格为（　  ）

（A）300元　  （B）900元　 （C）2400元　 （D）3600元

20．某种细菌在培养过程中，每15分种分裂一次（由1个分裂为2个），经过两小时，1个这种细菌可以分裂成（　 ）

（A）255个　 （B）256个　 （C）511个  （D）512个

二、填空题

1．若f(x)=在区间（-2，+）上是增函数，则a的取值范围是　　　　 。

2．若集合A={},B={　　　　 。

3.函数f(x)=log₍₂^x_-1)的定义域是　　　　 。

4．若点（1，2）既在f(x)=的图像上，又在f^-1(x)的图像上，则f^-1(x)=　　　　 。

5.设M=log时,它们的大小关系为　　　　 (用“<”连结起来)。

6．已知f(x)=　　　　 。

7.1992年底世界人口达到54.8亿，若人口的平均增长率为x%，2000年底世界人口数为y(亿)，那y与x的函数关系是　　　　 。

8．某工厂1995年12月份的产值是1月份的产值的a倍，那么1995年1至12月份的产值平均每月比上月增长的百分率是　　　　 。

9．某产品的总成本C（万元）与产量x(台)之间有函数关系式：C=3000+20x-0.1x²,其中x(0,240)。若每台产品售价为25万元，则生产者不亏本的最低产量为　　　　 台。

10．的定义域为R，则实数m的取值范围是________

一、

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20

二、1、___________2、__________3、____________

7、___________8、__________9、____________10、_________

三、解答题

1．已知函数f(x)=log[()^x-1],(1)求f(x)的定义域；（2）判断f(x)的单调性。

2、函数是定义在R上的函数且当时，求f(x)的解析式；并作出f(x)在R上的图象。

2．已知f(x)是对数函数，f()+f()=1,求f()的值。

4.设f(x)=x²-x+k,若log₂f(a)=2,f(log₂a)=K(a>0且a),求使f(log₂x)>f(1)且log₂f(x)<f(1)成立的x的取值范围。

5．20个下岗职工开了50亩荒地，这些地可以种蔬菜、棉花、水稻，如果种这些农作物每亩地所需的劳力和预计的产值如下：

每亩需劳力　　　每亩预计产值

蔬　菜　　　　  　　　　　　　　1100元

棉　花　　　　  　　　　　　　　 750元

水　稻　　　　  　　　　　　　　 600元

问怎样安排，才能使每亩地都种上作物，所有职工都有工作，而且农作物的预计总产值达到最高？

6．如图，在边长为4的正形ABCD的边上有一点P，从B点开始沿着正方形ABCD的边向点A（终点）移动，设点P移动的路程为x，△ABP的面积S=.

(1)求函数S的解析式。（6分）

(2)作出函数的图象.（4分）

7．某摩托车生产企业，上年度生产摩托车的投入成本为1万元/辆，出厂价为1.2万元／辆，年销售量为１０００辆，本年度为适应市场需求，计划提高产品档次，适度增加投入成本，若每辆车投入成本增加的比例为x(0<x<1)，则出厂价相应提高的比例为０.75x,同时预计年销售量增加的比例为0.6x，已知年利润＝（出厂价－投入成本）×年销售量。

（I）写出本年度预计的年利润y与投入成本增加的比例x的关系式。

（II）为使本年度的年利润y比上年有所增加，问投入成本增加的比例x应在什么范围内？

8．如果在1980年以后，每一年的工农业产值比上一年平均增加8%，那么到哪一年工农业产值可以翻两番？（lg2=0.3010,lg³-0.4771）

第六单元　 函数综合题

一、选择题

题号	1	2	3	4	5	6	7	8	9	10
答案	B	B	D	A	A	C	A	D	D	C
题号	11	12	13	14	15	16	17	18	19	20
答案	B	C	C	D	B	B	D	B	C	B

二、填空题

1．a>。　　f(x)=a+,f(x)在（-2，+）上是增函数，1-2a<0,解得a>

2.[ ,1]　　 A={x},B={x},B={x}∴AB=[,1](1,+)。

3.(0,1) 　 由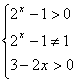联立解得0<x<且x

4.f^-1(x)=-x²(x0)。 由已知（1，2）和（2，1）都在f(x)=的图象上，则有

=, f^-1(x)=-x²(x0)

5.N<P<M。

6．-2　 由

7．Y=54.8×(1+x%)⁸　　　  8.100()%

9.150

设生产者不亏本的最低产量为x万元，则由题意，25x-(3000+20x-0.1x²)0,即x²+50x-300000.

∴　x150或x-200,又 ∵x(0,240), ∴x150。

10．　　

设a与各数据的差的平方和为m,即m=(a-a₁)²+(a-a₂)²+…+(a-a_n)²=na²-2(a₁+a₂+…+a_n)a+a₁²+a₂²+…+a_n²=n(a-)²+(a₁²+a₂²+…+a²_n)-

∵ n>0,∵a=时,m取最小值。

三、解答题

1．（1）由（）^x-1>0,解得x<0∴f(x)的定义域为(-,0)

（2）设x₁,x₂(-,0)且x₁<x₂,则0<()<()

∴log[()-1]>log[()^x1-1],则f(x)在（-，0）上为增函数

2. ∵x₁,x₂是x²-2(m-1)x+m+1=0的两个实根，∴ =4（m-1）²-4(m+1)0,解得m或m3。

又∵x₁+x₂=2(m-1),x₁·x₂=2(m-1),x₁·x₂=m+1, ∴y=f(m)=x₁²+x₂²=(x₁+x₂)²-2x₁x₂=4m²-10m+2,即y=f(m)=4m²-10m+2(m0或m3)

3.设f(x)=log_ax,已知f(+1)+f(-1)=1,则log_a(+1)+log_a(-1)=log_a5=1, ∴f(+1)+f(-1)=log_a(+1)+log_a(-1)=log_a25=log_a5²=2log_a5=2。

4.已知log₂f(a)=2,则f(a)=4, ∴a²-a+k=4……①已知f(log₂a)=k,则log₂²a-log₂a+k=k, ∴log₂a(log₂a-1)=0,∵ log₂a0, ∴log₂a=1,则a=2……②,①②联立得a=2,k=2, ∴f(x)=x²-x+2

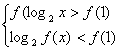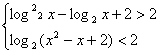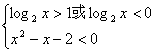已知 　　则有 　∴　 由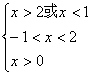　联立得0<x<1

5.设种蔬菜、棉花、水稻分别为x亩，y亩，z亩，总产值为u，依题意得x+y+z=50，，则u=1100x+750y+600z=43500+50x.∴ x0,y=90-3x0,z=wx-400,得20x30,∴当x=30时，u取得大值43500，此时y=0,z=20.∴安排15个职工种30亩蔬菜，5个职工种20亩水稻，可使产值高达45000元。

6．AB=2x, =x,于是AD=，因此，y=2x· +，即y=-。 由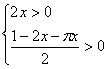，得0<x<函数的定义域为（0，）。

7．设销售价为50+x，利润为y元，则y=(500-10x)(50+x-40)=-10(x-20)²+9000,∴当x=20时,y取得最大值，即为赚得最大利润，则销售价应为70元。

 8．设经过x年可以翻两番，依题意得（1+8%）^x=4,即1.08^x=4,两边同时取常用对数，得x=就可以翻两番。