4.2 弧度制
【知识归纳】
1、弧度制使“角”与“实数”之间建立了一一对应关系，为三角函数奠定了基础。我们把等于半径长的圆弧所对的圆心角叫做1弧度的角。
2、
，
，
。
3、
，
，
。（“
”与“0”表示单位）。
4、已知扇形周长、面积，求扇形半径、圆心角。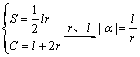
。
【基础训练】
1、把下列各角从度化成弧度：
（1）
=______（rad）； （2）
=__________；（3）
=__________；
（4）
=__________；（5）
=__________；（6）
=__________。
2、把下列各角从弧度化成度：
（1）
rad=______；（2）
rad=______；（3）
rad=______；（4）
rad=______；
（5）
rad=______；（6）
rad
______；（7）
=______；（8）3rad______。
3、把下列各角从度化成弧度：
（1）
=______________；（2）
=__________________；（3）
=______________；
（4）
=____________；（5）
=_________________；（6）
=______________。
4、把下列各角从弧度化成度：
（1）
rad=______；（2）
rad=______；（3）
rad=______；（4）
rad=______；
（5）
rad=______；（6）
rad=______；（7）
______；（8）
______。
5、用弧度制表示：
（1）终边在y轴负半轴上的角的集合： （2）终边在x轴上的角的集合：
（3）终边在二、四象限夹角平分线上的角的集合：（4）终边落在x轴上方的角的集合：
6、把下列各角化成0~2π的角加上
的形式，并指出它们是哪个象限的角：（要求既快又准）
（1）
=
（2）
=
（3）
=
（4）
=
（5）
=
（6）
=
（7）
=
（8）
=
7、半径为1m的圆中，600圆心角所对弧长为______，扇形面积为__________。
8、半径为120mm的圆上，有一条弧长为144mm，则此弧所对圆心角度数为_________。
9、直径为20cm的轮子以4rad/s（弧度/秒）速度旋转，则轮周上一点转5s所经过的弧长为______。
10、已知10的圆心角所对的弧长为1m，则这个圆的半径是_________。
11、已知长50cm的弧为2000，则这条弧所在圆的半径约为_________cm。
12、填表，求下列各角的值：（为下节准备）
| 0 |
|
|
|
| |
| 正弦（sinα） | |||||
| 余弦（cosα） | |||||
| 正切（tanα） |
13、将角
表示成
的形式为（ ）
（A）
（B）
（C）
（D）
14、把–14850化成
的形式是（ ）
（A）
（B）
（C）
（D）
15、将分针拨快10分钟，则分针转过的弧度数是（ ）
000000
（A）
（B）
（C）
（D）
16、若2弧度的圆心角所对的弧长4cm，则这个圆心角所夹的扇形的面积是（ ）
（A）4cm2 （B）2cm2 （C）4πcm2 （D）2πcm2
17、如果α与
具有同一条终边，β与
也具有同一条终边，那么α与β间的关系是（ ）
（A）
（B）
（C）
（D）
18、已知2弧度的圆心角所对的弦长为2，那么这个圆心角所对弧的弧长是（ ）
（A）2 （B）
（C）
（D）
19、已知
，
（
，α是锐角），则
与
的终边位置关系是（ ）
（A）关于x轴对称 （B）关于y轴对称 （C）关于原点对称 （D）重合
20、已知扇形的周长是6cm，面积为2cm2，则扇形的中心角的弧度数是（ ）
222222
（A）1 （B）4 （C）1或4 （D）2或4
**21、已知集合
，
，则A
B等于（ ）
（A）
（B）
（C）
（D）
**22、已知扇形面积为 S，扇形中心角为α，求扇形周长与中心角α的关系式。
4.2 弧度制
1、（1）
；（2）
；（3）
；（4）
；（5）
；（6）
.
2、（1）
；（2）；（3）
；（4）
；（5）；（6）
；（7）
；（8）
。
3、（1）
；（2）
；（3）
；（4）
；（5）
；（6）
.
4、（1）；（2）
；（3）
；（4）
；（5）
；（6）
；（7）
；（8）
。
5、（1）
；（2）
；（3）
；
（4）
。
6、（1）
；（2）
；（3）
；
（4）
；（5）
；（6）
；
（7）
；（8）
。
7、
，
。 8、1.2rad。 9、200cm。 10、
。 11、
。
12、略。
22、分析：扇形周长C=2l+r，条件中没有l，也没有r只有s，以及变量α，所以题目本质为用S与α表示l与r，所以考虑由公式
，变形得到。
解：∵，∴，∴
，∴
，∴
，∴
，
∴
。
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| C | D | B | A | D | C | A | C | D |