高一(上)数学单元同步练习
第二单元 简易逻辑
[重点]
理解逻辑联结词“或”、“且”“非”的意义,并会用它们构造复合命题,把握“若p则q”形式的复合命题,特别是会构造其逆命题、否命题、逆否命题;掌握四种命题及其关系;理解充分条件、必要条件、充要条件的意义,能够初步判断给定的两个命题的充要关系。
[难点]
对逻辑中的“或”、“且”的理解,特别是对一些代数命题真假的判断。
一、选择题
1.下列语句中是命题的是( )
(A)语文和数学 (B)sin45°=1
(C)x2+2x-1 (D)集合与元素
2.下列语句中的简单命题是( )
(A)![]() 不是有理数
(B)
不是有理数
(B)![]() ABC是等腰直角三角形
ABC是等腰直角三角形
(C)3X+2<0 (D)负数的平方是正数
3.已知下列三个命题
① 方程x2-x+2=0的判别式小于或等于零;②矩形的对角线互相垂直且平分;③2是质数,其中真命题是( )
(A)①和② (B)①和③ (C)②和③ (D)只有①
4.命题:“方程X2-2=0的解是X=![]() ”中使用逻辑联系词的情况是( )
”中使用逻辑联系词的情况是( )
(A)没有使用逻辑联结词 (B)使用了逻辑联结词“且”
(C)使用了逻辑联结词“或” (D)使用了逻辑联结词“非”
5.下列结论中正确的是( )
(A)命题p是真命题时,命题“P且q”定是真命题。
(B)命题“P且q”是真命题时,命题P一定是真命题
(C)命题“P且q”是假命题时,命题P一定是假命题
(D)命题P是假命题时,命题“P且q”不一定是假命题
6.语句![]() 或
或![]() 的否定是( )
的否定是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
7.使四边形为菱形的充分条件是( )
(A)对角线相等 (B)对角线互相垂直
(C)对角线互相平分 (D)对角线垂直平分
8.已知全集U=R,A![]() U,B
U,B![]() U,如果命题P:
U,如果命题P:![]() ,则命题非P是( )
,则命题非P是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
9.如果命题“非P为真”,命题“P且q”为假,那么则有( )
(A)q为真 (B)q为假
(C)p或q为真 (D)p或q不一定为真
10.如果命题“p或q”和命题“p且q”都为真,那么则有( )
(A)p真q假 (B)p假q真
(C)p真q真 (D)p假q假
11.若b>0,则![]() ( )
( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既非充分也非必要条件
12.下列四个命题
(1)面积相等的两个三角形全等 (2)在实数集内,负数不能开平方 (3)如果m2+n2![]() ,那么
,那么![]() (4)一元二次不等式都可化为一元一次不等式组求解。其中正确命题的个数是( )
(4)一元二次不等式都可化为一元一次不等式组求解。其中正确命题的个数是( )
(A)1 (B)2 (C)3 (D)4
13.在命题“若抛物线y=ax2+bx+c的开口向下,则{![]() }
}![]() ”的逆命题、否命题、逆否命题中结论成立的是( )
”的逆命题、否命题、逆否命题中结论成立的是( )
(A)都真 (B)都假 (C)否命题真 (D)逆否命题真
14.设![]() ABC的三边分别为a,b,c,在命题“若a2+b2
ABC的三边分别为a,b,c,在命题“若a2+b2![]() ,则
,则 ![]() ABC不是直角三角形”及其逆命题中有( )
ABC不是直角三角形”及其逆命题中有( )
(A)原命题真 (B)逆命题真
(C)两命题都真 (D)两命题都假
15.一个整数的末位数字是2,是这个数能被2整除的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
16.一个命题与它的逆命题、否命题、逆否命题这四个命题中( )
(A)真命题的个数一定是奇数 (B)真命题的个数一定是偶数
(C)真命题的个数可能是奇数也可能是偶数 (D)上述判断都不正确
17.如果a,b,c都是实数,那么P∶ac<0,是q∶关于x的方程ax2+bx+c=0有一个正根和一个负根的( )
(A)必要而不充分条件 (B)充要条件
(C)充分而不必要条件 (D)既不充分也不必要条件
18.下面命题中是真命题的为( )
(1)“x+y=5”是“x2-y2-3x+7y=10”的充分条件;(2)“a-b<0”是“a2-b2<0”的充分条件;(3)“a-b<0”是“a2-b2<0”的必要条件;(4)“两个三角形全等”是“两边和夹角对应相等”的充要条件
(A)①② (B)①③ (C)②③ (D)①④
19.如果p是q的充分条件,r是q的必要条件,那么( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
20.设⊙O1、⊙O2的半径分别为r1,r2,d=O1O2、, ⊙O1和⊙O2相交的充要条件是( )
(A)d<r1+r2
(B)d![]()
(C)![]() (D)d<r1+r2或d>
(D)d<r1+r2或d>![]()
二、填空题
1.分别用“p或q”,“p且q”,“非p”填空:
命题“非空集A![]() 中的元素既是A中的元素,也是B中的元素”是
的形式;命题“非空集A
中的元素既是A中的元素,也是B中的元素”是
的形式;命题“非空集A![]() B中的元素是A中元素或B中的元素”是
的形式;命题“非空集CUA的元素是U中的元素但不是A中的元素”是
的形式。
B中的元素是A中元素或B中的元素”是
的形式;命题“非空集CUA的元素是U中的元素但不是A中的元素”是
的形式。
2.命题“a,b都是奇数,则a+b是偶数”的逆否命题是 。
3.设甲是乙的充分而不必要条件,丙是乙的充要条件,丁是丙的必要而不充分条件,那么丁是甲的 条件。
4.A:x1,x2是方程ax2+bx+c=0(a![]() 0)的两实数根;B:x1+x2=-
0)的两实数根;B:x1+x2=-![]() ,则A是B的
条件。
,则A是B的
条件。
5.设P:![]() ABC是等腰三角形;q:
ABC是等腰三角形;q:![]() ABC的直角三角形,则“p且q”形式的复合命题是
ABC的直角三角形,则“p且q”形式的复合命题是
6.已知命题P:内接于圆的四边形对角互补,则P的否命题q是 。
7.在a=b,a=-b,![]() 中,使a2=b2的充分条件是
中,使a2=b2的充分条件是
8.命题“不等式x2+x-6>0的解x<-3或x>2”的逆否命题是
9.如果a、b、c都是实数,那么P:ac<0,是q:关于x的方程ax2+bx+c=0有一正根和一个负根的 条件。
10.命题“各位数字之和是3的倍数的正整数,可以被3整除”与它的逆命题、否命题、逆否命题中,假命题的个数为 ;真命题的个数为 ;真命题是 。
三、解答题
1.将下列命题改写成“若p则q”的形式,并写出其逆命题、否命题、逆否命题。
(1) 正数a的平方根不等于0;
(2)两条对角线不相等的平行四边形不是矩形。
2.求关于x的二次方程x2-mx+m2-4=0有两个不相等的正实根的充要条件。
3.用反证法证明:不存在整数m,n,使得m2=n2+1998
4.命题“当a<-b<1时,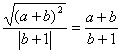 ”是否正确?为什么?
”是否正确?为什么?
5.求证:关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0
6.求证:关于x的一元二次不等式ax2-ax+1>0对于一切实数x都成立的充要条件是0<a<4
7.当a>0,b>0时,用反证法证明![]() ,并指出等号成立的充要条件。
,并指出等号成立的充要条件。
8.设平面上有六个圆,每个圆的圆心都在其余各圆的外部,试用反证法证明平面上任一点都不会同时在这六个圆的内部。
第二单元 简易逻辑
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | B | C | B | D | D | C | D | C |
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | B | A | D | B | A | B | B | D | B | C |
一、填空题
1.p且q,p或q,非p 2.a+b不是偶数,则a、b不都是奇数 3.必要而不充分条件
4.充分而不必要条件 5.![]() ABC是等腰直角三角形 6.不内接于圆的四边形对角不互补 7.a=b,或a=-b或
ABC是等腰直角三角形 6.不内接于圆的四边形对角不互补 7.a=b,或a=-b或![]() 8.若x
8.若x![]() ,则x2+x-6
,则x2+x-6![]() 9.充分必要条件 10.0;4;原命题、逆命题、否命题、逆否命题
9.充分必要条件 10.0;4;原命题、逆命题、否命题、逆否命题
三、解答题
1.(1)“若a是正数,则a的平方根不等于0”逆命题是:“若a的平方根不等于0,则a是正数”,否命题是“若a不是正数,则它的平方根等于0,”逆否命题:“若a的平方根等于0,则a不是正数”。
(2)“若平行四边形的两条对角线不相等,则它不是矩形”,逆命题是:“若平行四边形不是矩形,则它的两条对角线不相等”,否命题是“若平行四边形的两条对角线相等,则它是矩形逆否命题是:“若平行四边形是矩形,则它的两条对角线相等。”
2.由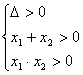 即
即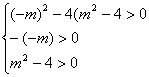 得
得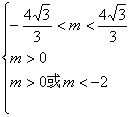 ∴
∴![]() 2<m<
2<m<![]()
3.假设存在整数m、n使得m2=n2+1998,则m2-n2=1998,即(m+n)(m-n)=1998。
当m与n同奇同偶时,m+n,m-n 都是偶数,∴ (m+n)(m-n)能被4整除,但4不能整除1998,此时(m+n)(m-n)![]() ;
;
当m,n为一奇一偶时,m+n 与m-n 都是奇数,所以(m+n)(m-n)是奇数,此时(m+n)(m-n) ![]() 。
。
∴假设不成立则原命题成立。
4.不正确
![]() a<-b<1, ∴a+b<0且b+1>0
a<-b<1, ∴a+b<0且b+1>0
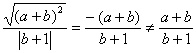
5. (1)充分性:![]() a+b+c=0, ∴a·12+b·1+c=0, ∴x=1是方程ax2+bx+c=0的一个根
a+b+c=0, ∴a·12+b·1+c=0, ∴x=1是方程ax2+bx+c=0的一个根
(2)必要性:![]() x=1是方程ax2+bx+c=0的根,∴a·12+b·1+c=0,即a+b+c=0综合(1)(2),关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0
x=1是方程ax2+bx+c=0的根,∴a·12+b·1+c=0,即a+b+c=0综合(1)(2),关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0
6.(1)必要性:若ax2-ax+1>0对x![]() 恒成立,由二次函数性质有:
恒成立,由二次函数性质有:![]()
即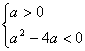 ∴0<a<4
∴0<a<4
(2)充分性:若0<a<4,对函数y=ax2+ax+1,其中![]() 且a>0 ∴ax2-ax+1>0(X
且a>0 ∴ax2-ax+1>0(X![]() R)恒成立。
R)恒成立。
由(1)(2)命题得证。
 7.假设
7.假设![]() <
<![]() ,则a+b<2
,则a+b<2![]() ),(
),(![]() )2<0这与(
)2<0这与(![]() )2
)2![]()
![]()
![]() 0,相矛盾
0,相矛盾![]() ,其中等号成立的充要条件是a=b。
,其中等号成立的充要条件是a=b。
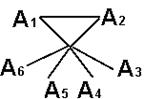
8.设六个圆的圆心分别为A1、A2……A6,假设点P同时在它们的内部,依题意得PA1<A1A2,PA2<A1A2
∴ ![]() A1PA2为
A1PA2为![]() A1PA2 的最大内角 ∴
A1PA2 的最大内角 ∴![]() A1PA2>60°,同理可证
A1PA2>60°,同理可证![]() A2PA3>60°,∴……
A2PA3>60°,∴……![]() A6PA1>60°
A6PA1>60°![]() A1PA2+……+
A1PA2+……+![]() A6PA3+…+
A6PA3+…+![]() A6PA1>360°,与周角定义相矛盾,故点P不能同时在这六个圆的内部。
A6PA1>360°,与周角定义相矛盾,故点P不能同时在这六个圆的内部。