高一下 4.1 角的概念的推广同步练习
基础练习
1．判断下列命题是否正确，并说明理由：
（1）小于90°的角是锐角；
（2）第一象限角小于第二象限角；
（3）终边相同的角一定相等；
（4）相等的角终边一定相同；
（5）若a∈〔90°，180°〕，则a 是第二象限角．
2．已知角的顶点与直角坐标系的原点重合始边与x轴的正半轴重合，作出下列各角，并指出它们是哪个象限的角：
（1）495° （2）－105° （3）780° （4）－390°
3．在0°~360°的范围内，找出与下列各角终边相同的角，并判定下列各角是哪个象限的角：
（1）1400° （2）－950°20′ （3）－1519°
4．和－463°终边相同的角可以表示为（ ）．
A．k·360°＋463°，k∈Z
B．k·360°＋103°，k∈Z
C．k·360°＋257°，k∈Z
D．k·360°－257°，k∈Z
5．经过一个小时，手表上的时针旋转了（ ）．
A．30° B．－30° C．15° D．－15°
6．在－720°到720°之间与－1020°终边相同的角有________．
7．与－3920°终边相同的最小正角是________．
8．如图4－1所示，如按逆时针旋针，终边落在OA位置时的角的集合是________；终边落在OB位置时的集合是________．
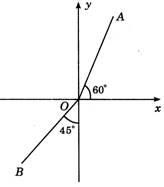
图4－1
综合练习
1．判断下列命题是否正确，并说明理由：
（1）集合P＝｛锐角｝，集合Q＝｛小于90°的角｝，则有P＝Q；
（2）角a 和角2a 的终边不可能相同；
（3）在坐标平面上，若角β的终边与角a 终边同在一条过原点的直线上，则有b ＝kp＋a ，k∈Z；
（4）若a 是第二象限角，则2a 一定是第四象限角；
（5）设集合A＝{射线OP}，集合B ＝{坐标平面内的角}，法则f：以x轴正半轴为角的始边，以OP为角的终边，那么对应f：OP∈Ａ→
是一个映射；
（6）不相等的角其终边位置必不相同．
2．判断下列各角哪些是同终边的角：
（1）－75°； （2）105°；（3）285°； （4）－315°； （5）405°（6）－615°
3．角的顶点在坐标系的原点，始边与x轴的正半轴重合，那么终边在下列位置的角的集合分别是：
（1）x轴负半轴________； （2）坐标轴上________；
（3）直线y＝x________； （4）两坐标轴及y＝±x________．
4．时钟的分针经过1小时10分钟，它所转的角是________度．
5．“x是钝角”是“x是第二象限角”的（ ）．
A．充分非必要条件 B．必要非充分条件
C．充分必要条件 D．即不充分也不必要条件
6．S是与－374°15′终边相同的角的集合，M＝{b｜｜b｜＜360°＝，则
＝（ ）．
A．S B．{14°15′}
C．{14°15′，－14°15′} D．{－14°15′，345°45′}
7．若a 是第四象限角，则
是（ ）．
A．第二象限角 B．第三象限角
C．第一或第三象限角 D．第二或第四限角
8．设a 是第二象限角，则
的终边不在（ ）．
A．第一象限 B．第二象限 C．第三象限 D．第四象限
参考答案
基础练习
1．（1）不正确．小于90°的角包含负角．
（2）不正确．反例：390°是第一条象限角，120°是第二象限角，但390°＞120°．
（3）不正确．它们彼此可能相差2p的整数倍．
（4）正确．此角顶点在坐标原点，始边与x轴正半轴重合的前提下．
（5）不正确．90°、180°均不是象限角．
2．
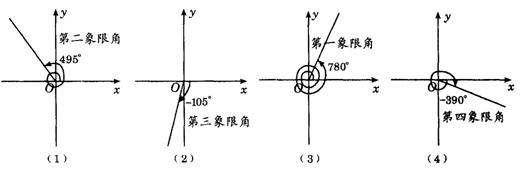
图答4－1
3．（1）320°，第四象限角 （2）129°40′，第二象限角 （3）281°，第四象限角
4．C．－463°与257°终边相同．
5．B．时针是顺时针方向旋转，故应为负角．
6．－660°、－300°、60°、420°． 与－1020°终边相同角为60°+360°k，令－720°＋360°k＜320°，解得
，又k∈Z，故k＝－2、－1、0、1．
7．40°．
8．
．
综合练习
1．（1）不正确．小于90°的角包含负角．
（2）不正确．如
，则a 与2a 终边相同．
（3）正确．
（4）不正确．也可能是第三象限的角．
（5）不正确．以OP为终边的∠xOP不唯一．
（6）不正确．终边相同角未必相等．
2．（1）与（3）同终边； （2）与（6）同终边； （4）与（5）同终边．
3．（1）
（2）
；
（3）
；
（4）
．
4．－420． 5．Ａ． 6．D 7．D．
8．C．360°·k＋90°＜a＜360°·k＋180°，则120°·k＋30°＜
＜120°·k＋60°，如图答4－2，角终边不在第三象限．
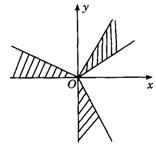
图答4－2