| 学 科 | 数学 | 版 本 | 人教版大开本、3+X | 期 数 | 2340 |
| 年 级 | 高一 | 编稿老师 | 梁文莉 | 审稿教师 |
|
【同步教育信息】
一. 本周教学内容:
§5.10 解斜三角形应用举例
§5.11 实习作业
目标:
使学生掌握利用正弦定理和余弦定理解任意三角形的方法,懂得解任意三角形的知识在实际中有着广泛的应用,从而培养学生分析问题、解决问题的能力;进一步巩固学生所学知识,提高分析和解决简单的实际问题的能力、动手操作的能力以及用数学语言表达实习过程和实习结果的能力,增强用数学的意识。
二. 重点、难点:
重点:利用正弦定理、余弦定理等知识解决实际问题。
难点:将实际问题转化成数学问题,利用正弦定理、余弦定理或有关数学方法解斜三角形。
三. 学法指导:
在生产和实际生活中,有时会遇到测量、航海、物理等方面的问题,处理这一类问题一般要用到解三角形的知识,解题时首先要认真分析题意,画出示意图,将该实际问题转化成数学问题,然后利用正弦定理、余弦定理及相关知识和方法解决问题。在计算过程中,要注意实际问题的计算精度要求,利用近似计算的规则,要做到算法简练,算式工整,计算准确。
【典型例题】
例1. ![]()
![]()
![]()

分析:![]()
个三角形中,除AB的另外两边也都是未知的,需要在其他三角形中找出合适的关系式,求出它们的值。
解:![]()
![]()
![]()
![]()
由正弦定理可得
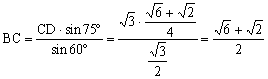
在![]() 中,由余弦定理得
中,由余弦定理得
![]()
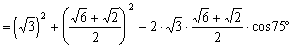
![]()
![]()
![]()
![]()
说明:(1)解斜三角形的重要工具是正弦定理、余弦定理;(2)测量不能直达的两点间的距离,利用解斜三角形是一个重要方法,解决这类问题的关键是构造一个或几个三角形,测出有关的边长和角,再如本例一样用正、余弦定理进行计算。
例2. 如图(2)所示,海中小岛A周围38海里内有暗礁,船向正南航行,在B处测得小岛A在船的南偏东30°,船行30海里后,在C处测得小岛A在船的南偏东45°,如果此船不改变航向,继续向南航行,有无触礁的危险?
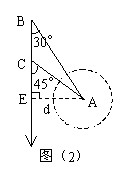
分析:如何判断小船有无触礁的危险?只要看小岛A到BC所在直线的距离d是否大于38海里,若d≥38海里,则小船没有触礁的危险,若d<38海里,则小船就有触礁的危险。怎样求小岛A到BC所在直线的距离d呢?过A作AE⊥BC于点E,则d=AE。AE可以在△ACE或△ABE中找关系式求解。但不管哪一个三角形,各边都是未知的量,需要在其他三角形中找出合适的关系式求解。
解:过A作AE⊥BC于点E。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
说明:在运用解斜三角形知识解决有关实际问题时,要注意阅读理解,弄清题意,特别要弄清类似于方位角等术语的含义,画出示意图,分析与所求问题有关的三角形,利用正、余弦定理求解。
例3. 如图(3),地平面上有一旗杆OP,为了测得它的高度h,在地面上选一基线AB,
![]()
![]()
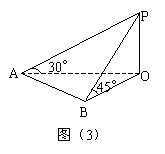
分析:在看图时要注意结合实际——旗杆OP垂直地面,所以△AOP和△BOP都是直角三角形。又这两个三角形中各已知一个锐角,那么其他各边均可用h的代数式表示。在△AOB中,已知一边及其对角,另两边均为h的代数式,可利用余弦定理构造方程,解这个方程即求出旗杆高h。
解:![]()
![]()
![]()
![]()
由余弦定理得:
![]()
![]()
![]()
答:旗杆高度约为13 m。
说明:(1)仰角和俯角是在同一铅垂面内视线与水平线的夹角,当视线在水平线之上时,称为仰角,当视线在水平线之下时称为俯角。
(2)由余弦定理(正弦定理)构造方程,是解决此问题的关键。方程思想是解决问题的一种常用思想方法。
例4. 我舰在敌岛A南偏西50°相距12海里的B处,发现敌舰正由岛沿北偏西10°的方向以10海里/时的速度航行。问我舰需以多大速度,沿什么方向航行才能用2小时追上敌舰?
分析:先根据方位角画出图,根据题意及所画出的方位图可知本题实际上可归纳为已知三角形的两边和它们的夹角,求第三边及角,
![]()
![]()
由BC长进而可求出我舰航行速度,由∠ABC的大小进而可求出我舰航行的方向。

解:![]()
由余弦定理得:
![]()
![]()
![]()
![]()
![]()
![]()
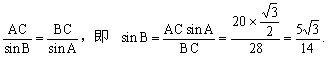
![]()
![]()
说明:解斜三角形应用题的一般步骤是:
(1)理解题意,分清已知与未知,画出示意图;
(2)根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学问题(或数学模型)。
(3)利用正弦定理或余弦定理有序地解出三角形,求得数学问题的解。
(4)检验上述所求的解是否符合实际意义,从而得出实际问题的解。
【模拟试题】
一. 选择题:
1. 从A处望B处的仰角为![]() ,从B处望A处的俯角为
,从B处望A处的俯角为![]() ,则
,则![]() 的关系为( )
的关系为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 海上有A、B两个小岛相距10海里,从A岛望C岛和B岛成![]() 的视角,从B岛望C岛和A岛成
的视角,从B岛望C岛和A岛成![]() 的视角,则B、C间的距离是( )
的视角,则B、C间的距离是( )
A. ![]() 海里 B.
海里 B. ![]() 海里 C.
海里 C. ![]() 海里 D.
海里 D. ![]() 海里
海里
3. 某人朝正东方向走![]() km后,向右转
km后,向右转![]() ,然后朝新方向走3km,结果他离出发点恰好
,然后朝新方向走3km,结果他离出发点恰好![]() km,那么
km,那么![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D. 3
D. 3
4. 在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为![]() ,则塔高为( )
,则塔高为( )
A. ![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D. 200米
米 D. 200米
5. 一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西![]() ,另一灯塔在船的南偏西
,另一灯塔在船的南偏西![]() ,则这只船的速度是每小时( )
,则这只船的速度是每小时( )
A. 5海里 B. ![]() 海里 C. 10海里 D.
海里 C. 10海里 D. ![]() 海里
海里
二. 填空题:
6. 一树干被台风吹断折成与地面成![]() 角,树干底部与树尖着地处相距20米,则树干原来的高度为___________.
角,树干底部与树尖着地处相距20米,则树干原来的高度为___________.
7. 某舰艇在A处测得遇险渔船在北偏东![]() 距离为10海里的C处,此时得知,该渔船沿北偏东
距离为10海里的C处,此时得知,该渔船沿北偏东![]() 方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是___________.
方向,以每小时9海里的速度向一小岛靠近,舰艇时速21海里,则舰艇到达渔船的最短时间是___________.
三. 解答题:
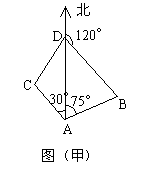
8. 如图(甲),某货轮在A处看灯塔,灯塔B在货轮的北偏东![]() ,距离为
,距离为![]() 海里,灯塔C在货轮的北偏西
海里,灯塔C在货轮的北偏西![]() ,距离为
,距离为![]() 海里,货轮由A处向正北航行到D处,再看灯塔B在北偏东
海里,货轮由A处向正北航行到D处,再看灯塔B在北偏东![]() ,求:(1)A处与D处的距离;(2)灯塔C与D处的距离。(精确到1海里)
,求:(1)A处与D处的距离;(2)灯塔C与D处的距离。(精确到1海里)
9. 在某时刻,A点西400千米的B处是台风中心,台风以每小时40千米的速度向东北方向直线前进,以台风中心为圆心、300千米为半径的圆称为“台风圈”,从此时刻算起,经过多长时间A进入台风圈?A处在台风圈中的时间有多长?
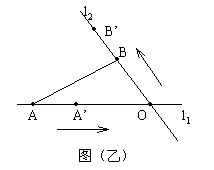
10. 为进行科学实验,观测小球A、B在两条相交成![]() 角的直线型轨道上运动的情况,如图(乙)所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道
角的直线型轨道上运动的情况,如图(乙)所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道![]() 按箭头的方向运动。问:
按箭头的方向运动。问:
(1)运动开始前,A、B的距离是多少米?(结果保留三位有效数字)。
(2)几分钟后,两个小球的距离最小?

【试题答案】
1. B 2. D 3. C 4. A 5. C
提示:
1. 如图所示:
2. 如图:

![]()
3. 如图:

设此人从A出发,则![]()
由正弦定理得 ![]()
![]()
![]()
4. 如图:
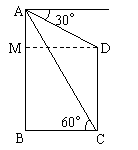
设AB为山高,CD为塔高,
则![]()
![]()
![]()
![]()
5. 如图:A、B为两灯塔,船由C向正北航行半小时后到达D,
则![]()
![]()
![]()

6. ![]() 米
米
提示:如图:
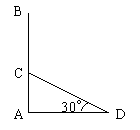
设树干AB在C处折断后树尖在D处,则![]()
![]()
![]()
7. ![]() 小时
小时
提示:如图,在![]() 中,
中,![]()
设舰艇到达渔船的最短时间为t,则![]() ,
,![]() ,由余弦定理得
,由余弦定理得
![]()
解得 ![]()
8. (1)在![]() 中,
中,![]() ,
,
![]()
由正弦定理得 ![]()
![]()
(2)在![]() 中,由余弦定理得
中,由余弦定理得
![]()
![]() 灯塔C与D处的距离约是14海里。
灯塔C与D处的距离约是14海里。
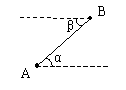
9. 如图,以AB为边,B为顶点作![]() (点P在B点的东北方向上),射线BP即台风中心B的移动方向,以A点为圆心、300千米为半径画弧交射线BP于C、D两点,显然当台风中心从B点到达C点时,A点开始进入台风圈,台风中心在CD上移动的时间即为A处在台风圈中的时间。设台风中心由B到C要t小时,在
(点P在B点的东北方向上),射线BP即台风中心B的移动方向,以A点为圆心、300千米为半径画弧交射线BP于C、D两点,显然当台风中心从B点到达C点时,A点开始进入台风圈,台风中心在CD上移动的时间即为A处在台风圈中的时间。设台风中心由B到C要t小时,在![]() 中,
中,![]() (千米),
(千米),![]() (千米),
(千米),![]() (千米),
(千米),![]() ,由余弦定理得,
,由余弦定理得,
![]()
即 ![]()
![]()
![]()
![]()
答:经过4.6小时A进入台风圈,A处在台风圈中的时间为5小时。
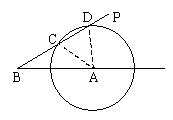
10. (1)小球开始运动前的距离为:
![]()
(2)设t分钟后,小球A、B分别运动到A’、B’处,则![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
故 ![]()
![]()
![]() 当
当![]() ,
,![]()
故![]() 分钟后两个小球的距离最小。
分钟后两个小球的距离最小。
| 年级 | 高一 | 学科 | 数学 | 版本 | 人教版大开本、3+X | 期数 | 2340 | |||||
| 内容标题 | 解斜三角形应用举例 实习作业 | |||||||||||
| 分类索引号 | G.623.3 | 分类索引描述 | 学习资料 | |||||||||
| 主题词 | 解斜三角形应用举例 实习作业 | 栏目名称 | 同步课堂 | |||||||||
| 编稿老师 | 梁文莉 | 审稿老师 | ||||||||||
| 录入 | 吕春艳 | 一校 | 康纪云 | 二校 | 王佳娣 | 审核 | ||||||