高一数学测试题—绝对值不等式一元二次不等式的解法(3)
一、选择题:
1、不等式0<2x-1<2的解集是 ( )
A.{x-![]() < x<
< x<![]() 或
或![]() <x<
<x<![]() }
B.{x-
}
B.{x-![]() <x<
<x< ![]() 且
且 ![]() <x<
<x< ![]() }
}
C.{x-![]() <x<
<x<![]() }
D.{x-
}
D.{x- ![]() <x<0或0<x<
<x<0或0<x< ![]() }
}
2、设集合A={xx<1}, B={xx>-1},则下列结论中错误的是 ( )
A.A ![]() B B.A∪B=A C.A∪B=R
D.A∩B=A
B B.A∪B=A C.A∪B=R
D.A∩B=A
3、不等式2x-1<2-3x的解集为 ( )
A.{xx<![]() 或x>1} B.{xx<
或x>1} B.{xx< ![]() }
}
C.{xx<![]() 或
或 ![]() <x<
<x< ![]() } D.{x-3<x<
} D.{x-3<x<![]() }
}
4、已知集合A={xx+2≥5},B={x-x2+6x-5>0},则A∪B等于 ( )
A.R B.{xx≤-7或x≥3}
C.{xx≤-7或x>1} D.{x3≤x<5}
5、如果不等式ax2+bx+c>0(a≠0)的解集是空集,那么下列条件中正确的是 ( )
A.a<0且b2-4ac<0 B.a<0且b2-4ac>0
C.a<0且b2-4ac≤0 D.a<0且b2-4ac≥0
6、若不等式ax2+bx+2<0的解集为{xx<- ![]() 或x>
或x>![]() },则
},则![]() 的值为 ( )
的值为 ( )
A.
![]() B.
B. ![]() C.—
C.—![]() D.—
D.— ![]()
7、不等式ax2 +bx+c>0的解是0<α<x<β,则不等式cx2- bx +a>0的解为 ( )A.![]() <x<
<x<![]() B.-
B.-![]() <x<—
<x<— ![]() C.-
C.-![]() <x<-
<x<-![]() D.
D. ![]() < x<
< x<![]()
8、己知关于x的方程(m+3)x 2-4mx +2m-1= 0 的两根异号,且负根的绝对值比正根大,那
么实数m的取值范围是
A.-3< m<0 B.0<m<3 C.m<- 3或m> 0 D.m<0 或 m>3
二、填空题:
9、不等式(a-2) x2 +2(a-2) x- 4<0对一切x ∈R恒成立,则实数a的取值范围 ___ . 10、若不等式2x- 1> m(x2- 1)对满足 -2 ≤ x ≤2 的所有m都成立,则x的取值范围是
.
11、不等式0 ≤x2 + m x+5 ≤3恰好有一个实数解,则m的取值范围是 .
12、不等式 x 2-3x -3≤1的解集为_______ .
三、解答题:
13、解不等式
(1)|x 2 -4x+2|≥
![]() ;
;
(2)||x+3|-|x-3||>3.
14、 解下列不等式:
① x 2-(a+1)x+a<0, ② a x2- 2ax+a- 3 ≤0 ;
15、设A={xx2 +3k2 ≥ 2 k (2x -1)},B={x x2- (2x-1)k + k2≥0}且A![]() B,试求k的
取值范围.
B,试求k的
取值范围.
16、
己知函数f (x) = ax2 +bx+c的图象经过点(-1,0),且不等式 x≤ f(x) ≤![]() (1+x 2 )对任
意x ∈ R恒成立,求函数f (x)的解析表达式.
(1+x 2 )对任
意x ∈ R恒成立,求函数f (x)的解析表达式.
高一数学测试题—参考答案
绝对值不等式与一元二次不等式的解法
一、ABBCC ACA
二、(9)![]() (10)
(10)![]() (11)m=±2(12)
(11)m=±2(12)![]()
三、(13)(1)(用性质脱去绝对值符号)原不等式等价于![]()
∴原不等式的解集为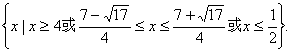 (2)解法一:(采用分区间法脱去绝对值符号):原不等式同解于下面三个不等式组:
(2)解法一:(采用分区间法脱去绝对值符号):原不等式同解于下面三个不等式组:
(1)![]() ;
;
(3)![]() ∴原不等式的解集为
∴原不等式的解集为![]() .解法二:(用平方法脱去绝对值符号):对原不等式两边平方,得
.解法二:(用平方法脱去绝对值符号):对原不等式两边平方,得![]() 两边再平方得
两边再平方得![]()
(14)解:①原不等式可化为:![]() 若a>1时,解为1<x<a,若a>1时,解为a<x<1,若a=1时,解为
若a>1时,解为1<x<a,若a>1时,解为a<x<1,若a=1时,解为![]() ②当a=0时,不等式为3
②当a=0时,不等式为3![]() 成立.解为R.当a<0时,由求根公式可得
成立.解为R.当a<0时,由求根公式可得
![]() 所以解为
所以解为![]() 当a<0时,方程的判别式为
当a<0时,方程的判别式为![]() ,故解为R.综上所述:当a
,故解为R.综上所述:当a![]() 时,解为R.当a<0时,解为
时,解为R.当a<0时,解为![]()
(15)解:![]() ,比较
,比较
![]() (1)当k>1时,3k-1>k+1,A={xx≥3k-1}或x
(1)当k>1时,3k-1>k+1,A={xx≥3k-1}或x![]() 分解(2)当k=1时,x
分解(2)当k=1时,x![]() .(3)当k<1时,3k-1<k+1 A=
.(3)当k<1时,3k-1<k+1 A=![]() B中的不等式不能因式,故考虑判断式
B中的不等式不能因式,故考虑判断式![]() 当k=0时,
当k=0时,![]() .(2)I当k>0时,△<0,x
.(2)I当k>0时,△<0,x![]() (3)当k<0时,
(3)当k<0时,![]() 当
当![]() 时,由B=R,显然有A
时,由B=R,显然有A![]() ,当k<0时,为使A
,当k<0时,为使A![]() ,需要
,需要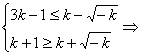 k
k![]() ,于是k
,于是k![]() 时,
时,![]() 综上所述,k的取值范围是:
综上所述,k的取值范围是:![]()
(16)解:由题意可知f(-1)=0,有a-b+c=0,……(1)又不等式![]() 对x R 恒成立,取x=1即成立,则有
对x R 恒成立,取x=1即成立,则有![]() 由(1),(2)得
由(1),(2)得![]()
由题条件:对![]() 恒成立,
恒成立,![]() 对
对![]() 恒成立.即
恒成立.即![]() 且
且![]() 对
对![]() 恒成立.所以有
恒成立.所以有
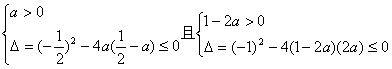 解得
解得 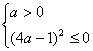 且
且
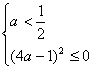 ∴得 a= c=
∴得 a= c= ![]() 求函数 f(x)=
求函数 f(x)=![]()