两角和与差的三角函数

两角和与差的三角函数

(时间60分, 满分100分)

一、选择题(每小题6分,共36分)

　　　　　　　　 [　　 ]
　A.充分不必要条件　 B.必要不充分条件
　C.充要条件　 　　　 D.既不充分也不必要条件

　　　　　　　　　　　　　　　 [　　 ]
　A.sin21　　 B.-sin21　　 C.cos21　　 D.-cos21

3.cos36°+cos108°的值为　 　　　　　　　　　　　　　　　　　　　 [　　 ]
　

　　　　　　　 　 [　　 ]
　

[　　 ]
　 

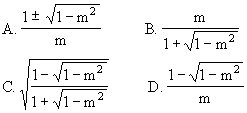
6.根据下列条件解△ABC,其中只有一个解的是　　　　　　　　　　　 [　　 ]
　A.a=15,b=16,A=95° 　
　
　
　D.a=4,b=5,A=30°　

二、填空题(每小题6分,共24分)

 

4.已知△ABC中,A=60°,B=75°,a=36,则c=　　　　　　　　 .　

三、解答题(每小题10分,共40分)

 
求:cos(α+β)的值.

　

3.已知:cos(θ-α)=a,sin(θ-β)=b.
求证:cos2(α-β)=a2+b2-2absin(α-β)

4.水塔(CD)高30米,从塔顶C测得河对岸两个目标A、B的俯角分别为30°和
45°,又塔底D对A、B的视角∠ADB=150°,求A、B的距离.

参考答案

　

一、1.B　 2.A　 3.B　 4.B　 5.C　 6.C

二、
1.2cosθ
2. 4
3.secα
　

三、
1.解:根据已知条件,



　

2.证明:
 
=tg2x-tgx=右边
∴原式成立.

3.证明:由已知得
cosθcosα+sinθsinα=a……①
sinθcosβ-cosθsinβ=b……②
①×sinβ+②×cosα,得
sinθ·cos(α-β)=asinβ+bcosα……③
①×cosβ-②×sinα,得
cosθ·cos(α-β)=acosβ-bsinα……④
③2+④²,得
cos2(α-β)=a2+b2+2ab(sinβcosα-cosβsinα)
=a2+b²-2absin(α-β)　

4.解:根据题意,图中

 
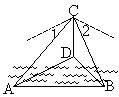
CD=30m,CD⊥平面ABD,
∠1=30°,∠2=45°,∠ADB=150°.
 
Rt△BCD中,BD=CD=30.
∵△ABD中,
AB2=AD²+BD2-2AD·BDcos150°
 
=900×7