高一数学期末综合测试（4）

高一数学期末综合测试（4）　　　　　　　　　　　　　 姓名　　　　

一、选择题：1.tan67.5⁰+tan22.5⁰的值为　　 A.　 B.2　 C.1　　D.不存在　　[　 ]

2.、是夹角为60⁰的单位向量,则=2+，=2-3的夹角为　　　　　　  [　 ]

  A.30⁰　　　　　　　 B.60⁰　　　　　　 C.120⁰　　　　  D.150⁰

3.根据下列条件解△ABC,则其中有两解的是　　　　　　　　　　　　　　　　　　　  [　 ]

  A.b=10 A=45⁰ C=70⁰　B.a=60 b=48 B=60⁰ C.a=7 b=5 A=80⁰　D.a=14 b=16 A=45⁰

4.若cosx=tanx,则sinx的值是　 A. B.-　C.　D.-　　 　[　 ]

5.已知O是△ABC所在平面内一点,若++=,且==,则△ABC是

  A.任意三角形　　　 B.直角三角形　　  C.等腰三角形　　　D.等边三角形　　　　 [　 ]

6.在△ABC中,=5,=8,·=20,则是　 A.6　B.7  C.8　D.9　　[　 ]

7.已知-＜β＜0＜α＜,cos(α-β)=,cos2α=-,则α+β的值为　　　　  　[　 ]

  A.　　　　　  B.　　　　　　 C.　　　　　　  D.

8.已知为非零向量,且·=·,则有　　　　　　　　　　　　　　　　　  [　 ]

  A.=　　　　  B.⊥　　　　  C.(-)⊥　　 D.=或(-)⊥

9.若,共线,则必有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 [　 ]

  A.·= B.·= C.+=+ D.-=+

10.=1,=2,,夹角120⁰,则(+2)·(2+)的值为A.-5 B.5 C.-D.　[　 ]

二、填空题：11.已知=(3,4),=(2,-1)且+k与-垂直,则实数k的值　 　　；

12.若sinθcosθ＞0,则θ在　　象限；

13.在△ABC中,BC=5,CA=12,AB=13,则·=　　；

14.在△ABC中,若B=30⁰，AB=2，AC=2，则△ABC的面积S是　　　　；

三、解答题：15. 化简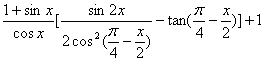

16.非零向量，满足==+，求与（-）的夹角θ

17.求证：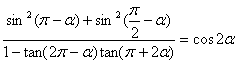

18.已知=(2,1),=(1,2),且⊥,∥,求.

19.已知=1，=，+=2，①求与的夹角，

　 ②是否存在实数t使(t-)⊥(+2).

20.在海港A正东39 nmile处有一小岛B，现甲船从A港出发以15 nmile/h的速度驶向B岛，

　 同时乙船以6 nmile/h的速度向北偏西30⁰的方向驶离B岛，不久之后，丙船则向正东方

　 向从B岛驶出，当甲乙两船相距最近时，在乙船上观测发现丙船在乙船南偏东60⁰方向上，

　 问：此时甲丙两船相距多远？