高一数学提高测试（二）

高一数学提高测试（二）

（90分钟，满分100分）

（一）选择题（每小题5分，共30分）

1．数列｛a_n｝中，a₁＝13，a₂＝56，a_n＋2＝a_n＋1－a_n，则a₁₉₉₉ 等于（　　）．

（A）－56　　（B）－43　　（C）13　　（D）－13

【提示】求出数列前若干项，分析其中的规律，其数值是周期性变化．

【答案】（C）．

2．若数列｛a_n｝前8项的值各异，且a_n＋8＝a_n 对任意的n N都成立，则下列数列中可取遍｛a_n｝前8项值的数列为（　　）．

（A）｛a_{2 k＋1}｝　　（B）｛a_{3 k＋1}｝　　（C）｛a_{4 k＋1}｝　　（D）｛a_{5 k＋1}｝

【提示】由已知，只需研究2 k＋1、3 k＋1、4 k＋1、5 k＋1被8除的余数是1到8的数．故3 k＋1型的数符合此条件．

【答案】（B）．

3．已知数列1，，，，，，，，，，…，则此数列前100项的和等于（　　）．

（A）13　　（B）13　　（C）14　　（D）14

【提示】将数列分成n 组：第一组：1，第二组：，，第三组，，，…，由于第n 组中有n 个数，且求前100项和，故令1＋2＋3＋…＋n＝100．即＝100，估值可知n＝13．即前13组中共有91个数，再加上第14组中前9个数，恰为100项，

【答案】（A）．

4．等差数列｛a_n｝的前m 项和为30，前2 m 项和为100，则它的前3 m 项和为（　　）．

（A）130　　（B）170　　（C）210　　（D）260

【提示】设前m 项和V₁，m＋1到2 m 项和V₂，2 m＋1到3 m 项和V₃，则V₁，V₂，V₃ 也成等差数列．于是V₁＝30，V₂＝70，d＝40．∴　V₃＝110．

【答案】（C）．

5．设｛a_n｝是由正数组成的等比数列，公比q＝2，且a₁·a₂·a₃·…a₃₀＝2³⁰，那么a₃·a₆·a₉·…·a₃₀ 等于（　　）．

（A）2¹⁰　  （B）2¹⁵　  （C）2¹⁶　  （D）2²⁰

【提示】设a₁·a₄·a₇·…·a₂₈＝x，则a₂·a₅·a₈·…a₂₉＝x·2¹⁰，a₃·a₆·a₉·…·a₃₀＝x·2²⁰．于是2³⁰＝x·（x·2¹⁰）·（x·2²⁰）＝x³·2³⁰，∴　x＝1．

【答案】（D）．

6．某露天剧场有28排座位，每相邻两排座位数相同，第一排有24个座位，以后每隔一排增加两个座位，则全剧场共有座位（　　）．

（A）1036个　　（B）1428个　　（C）854个　　（D）518个

【提示】由题意知第一、二排，第三、四排，…，第二十七，二十八排的座位数组成等差数列｛a_n｝，其中a₁＝24×2，d＝2×2，n＝14，则S₁₄ 可求．

【答案】（A）．

（二）填空题（每小题5分，共25分）

7．已知a＞b＞0，A 是a、b 的等差中项．G 是a、b 的等比中项，且G＞0，若A＝

2 G ．则a ︰b＝________________．

【提示】a＋b＝4，即＋＝4令＝x，则x＋＝4即x²－4 x＋1＝0，解得x＝2±而x＝＞1，∴　x＝2＋．

【答案】7＋4．

8．两个等差数列，它们的前n 项和之比为，则这两个数列的第九项的比是_________．

【提示】设两数列为｛a_n｝、｛b_n｝，相应的前n 项和为S_n、T_n 则＝，＝＝＝＝＝＝．

【答案】8︰3．

9．在数列｛a_n｝中，a₁＝1，S_n＝n²a_n ，则a_n＝______________．

【提示】当n≥2时，a_n＝S_n－S_n－1＝n²a_n－（n－1）² a_n－1

∴　＝，从而＝，＝，＝，…，＝，＝，将以上n－1个等式相乘，得＝．

【答案】a_n＝．

10．已知数列1，（1＋），（1＋＋），（1＋＋＋），…，（1＋＋＋…＋）．则此数列的前n 项和S_n＝______________．

【提示】∵　a_n＝1＋＋＋…＋＝2－

∴　S_n＝2 n－（1＋＋＋…＋）．

【答案】S_n＝2 n－2＋．

11．设n 个数成等比数列，P 是这n 个数的乘积，S 是这n 个数的和，S′是这n 个数的倒数和，那么P 等于______________．

【提示】P＝a₁ⁿ·，S＝．

S′＝·＝·．

∴　＝a₁²q^n－1，＝＝a₁ⁿ·＝P ．

【答案】P＝．

（三）解答题（第12小题12分，第13至15题每小题11分，共45分）

12．已知数列｛a_n｝中，S_n 是它的前n 项和，且S_n＋1＝4 a_n＋2，（n N），a₁＝1．

（1）设b_n＝a_n＋1－2 a_n，（n N），求证：数列｛b_n｝是等比数列；

（2）设c_n＝，（n N），求证：数列｛c_n｝是等差数列．

【提示】（1）由题意，得S_n＋2－S_n＋1＝4 a_n＋1－4 a_n，

即 a_n＋2＝4 a_n＋1－4 a_n，变形得a_n＋2－2 a_n＋1＝2（a_n＋1－2 a_n），

即 b_n＋1＝2 b_n，再由已知，b_n＝3·2^n－1

（2）由c_n＝，得c_n＋1－c_n＝，又 b_n＝3·2^n－1，故c_n＋1－c_n＝．

13．已知二次函数f（x）＝x²－2（10－3 n）x＋9 n²－61 n＋100（n N）

（1）设函数y＝f（x）图象的顶点的横坐标组成数列｛a_n｝，求数列｛a_n｝的通项公式a_n．

（2）设函数y＝f（x）图象的顶点到y 轴的距离构成数列｛b_n｝，求数列｛b_n｝的前n 项和．

【提示】（1）a_n＝10－3 n ．

（2）b_n＝a_n＝10－3 n＝

当n≤3时，S_n＝＝；

当n≥4时，S_n＝S₃＋b₄＋…＋b_n＝＋

＝．

14．已知等差数列｛a_n｝的首项为a₁＝21，公差d＝－4．

（1）若a₁＋a₂＋…＋a_k＝102，求k 的值；

（2）设｛a_n｝的前n 项和为S_n，试问数列｛S_n｝是否存在相同的两项，若存在，求出这样的两项，若不存在，说明理由．

【提示】（1）易知a_n＝25－4 n，令a_n≥0，则n≤6，即前6项为正数，从第7项开始为负数．

∴　a₁＋a₂＋…＋a_k＝（a₁＋a₂＋…＋a₆）－（a₇＋a₈＋…＋a_k）

＝2 k²－23 k＋132＝102．

解得 k＝10或（舍去）

（2）假设存在m，n（m，n N），使S_m＝S_n（m ≠n）．则可以推出2 m＋2 n＝23，对于m，n N，此式不可被成立，故｛S_n｝不存在相同的两项．

【答案】（1）k＝10；（2）不存在相同的两项．

15．已知数列｛a_n｝的通项公式，a_n＝（n＋1），问n 取何值时，a_n 取最大值．

【提示】方法一：不妨设a_n 最大，则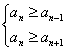，由此解得n＝8或9．

方法二：先分析｛a_n｝的单调性，a_n＋1－a_n＝·，再对n 分三类讨论，即n ＜8时；n＝8时，a_n 增函数，n＞8时，a_n 是减函数，进而得出结论．