高中学生学科素质训练
高一数学同步测试（6）—正、余弦函数的图象和性质
一、选择题（每小题5分，共60分，请将正确答案填在题后的括号内）
1．函数
在闭区间（ ）上为增函数. （ ）
A．
B．
C．
D．
2．函数
的单调减区间为 （ ）
A．
B．
C．
D．
3．设a为常数，且
，则函数
的最大值为
（ ）
A．
B．
C．
D．
4．函数
的图象的一条对称轴方程是 （ ）
A．
B．
C．
D．
5．方程
的实根有 （ ）
A．1个 B．2个 C．3个 D．无数个
6．下列函数中，以π为周期的偶函数是 （ ）
A．
B．
C．
D．
7．已知
的图象和直线y=1围成一个封闭的平面图形，该图形的面积
是 （ ）
A．4π B．2π C．8 D．4
8．下列四个函数中为周期函数的是 （ ）
A．y=3 B．
C．
D．
9．如果函数
的最小正周期为4π，那么常数ω为 （ ）
A．
B．2 C．
D．4
10．函数
的定义域是 （ ）
A．
B．
C．
D．
11．下列不等式中，正确的是 （ ）
A．
B．
C．
D．
12．函数
上为减函数，则函数
上
（ ）
A．可以取得最大值M B．是减函数
C．是增函数 D．可以取得最小值－M
二、填空题（每小题4分，共16分，答案填在横线上）
13．
为奇函数，
.
14．若
=
.
15．已知方程
有解，那么a的取值范围是
.
16．函数
的定义域为
.
三、解答题（本大题共74分，17—21题每题12分，22题14分）
17．已知
的最大值M（a）与最小值m（a）.
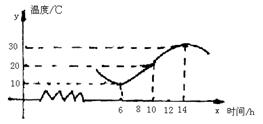
18．如图，某地一天从6时到11时的温度变化曲线近似满足函数
①求这段时间最大温差
|
19．已知
①求f（x）的最小正周期
②求f（x）的最值
③试求最小正整数k，使自变量x在任意两个整数间（包括整数本身）变化时，函数
f（x）至少有一个最大值，一个最小值.
20．已知函数
的最大值为1，最小值为－3，试确定
的
单调区间.
21．设
（1）令
表示P
（2）求t的取值范围，并分别求出P的最大值、最小值.
22．求函数
的定义域、值域、单调性、周期性、最值.
参考答案
一1．A 2．B 3．B 4．C 5．C 6．A 7．B 8．A 9．A 10．C 11．B 12．A
二、13．
14．
15．
16．
三、
17．（1）
（2）
（3）
（4）
18．（1）20° （2）
19．（1）
（2）
（3）k=2
20．（1）当a>0时，
（2）当a<0时，
在
21．（1）
（2）
22．定义域：
最小正周期：π 当
时递增
当
时
y没有最大值.