高中学生学科素质训练
高一数学同步测试（11）—第三章 数列的概念
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内。
1．数列11，13，15，
的项数为
（ ）
A．
B．
C．
D．
2．若
，则
的大小关系为
（ ）
A．
B．
C．
D．不能确定
3．在数列
中，
是它的
（ ）
A．第14项 B．第12项 C．第10项 D．第8项
4．已知数列
的首项
，且
，则
为 （ ）
A．7 B．15 C．30 D．31
5．已知数列的通项公式是
=
，则220是这个数列的 （ ）
A．第19项 B．第20项 C．第21项 D．第22项
6．中
，则值最小的项是
（ ）
A．第4项 B．第5项 C．第6项 D．第4项或第5项
7．已知
,则
的值为
（ ）
A．
B．
C．
D．
8．以下公式中:①
;②
;③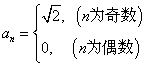
,可以作为数列
通项公式的是
（ ）
A．①② B．②③ C．①③ D．①②③
9．已知：数列，
，
，则
等于
（ ）
A．0 B．1 C．2 D．3
10．已知
，（
），则在数列｛｝的前50项中最小项和最大项分别是
（ ）
A．
B．
C． 
D．
二、填空题：请把答案填在题中横线上。
11．已知
，则和
等于
.
12．已知数列适合：
+
，则
++
.
13．观察数列的特点，并在空白处填上恰当的数：77，49，36， .
14．递增数列1，5，7，11，13，17，19，
。它包含所有既不能被2整除，又不能被3整除的正整数，则此数列的第100项为 .
三、解答题：解答应写出文字说明、证明过程或演算步骤。
15．根据数列的前几项，写出下列各数列的一个通项公式：
（1）1，
，
，
，……;
（2）
，
，
，
，……;
（3）1，
，
，
，
，……;
（4）9，99，999，9999，……;
（5）0，1，0，1，0，1，……；
（6）1，0，，0，，0，
，0，…….
16．已知函数
，数列{an}满足：a1=1，且
（1）写出数列的前5项，并猜想数列的表达式；
（2）若
，试求数列{bn}的前n项和Sn.
17．设数列中，，对所有的
，都有
.
（1）求
；（2）
是该数列的第几项？（3）试比较的大小.
18．设函数
，数列的通项满足
，⑴求数列的通项公式；⑵判定数列{a n }的单调性.
19．已知数列中，
，其中
.
（1）求
； （2）猜想数列的一个通项公式.
20．已知数列中，
（1）
，且
对任意n∈N*恒成立，求实数λ的取值范围；
（2）
，求常数
的值.
高一数学上学期测试题（11）参考答案
一、选择题：CBCDB DBDAC
二、填空题：
11．500； 12．161； 13．18； 14．
13．提示：
14．在数1～299中，有149个偶数，有能被3整除的数99个，能被6整除的数49个，故能被2或3整除的数有149+99
49=100个，从而.
三、解答题：
15．答案：⑴
；⑵
；⑶
； ⑷
；⑸
；
⑹（解一）：所给的数列可改写为
，数列的分子是1，0重复出现，
且奇数项为1，偶数项为0，所以可表示为
，分母的通项为，因此数列的一个通项公式为
；
（解二）数列的另一个通项公式为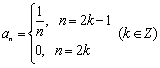
.
说明：① 表示数列，表示数列中的第项，= 
表示数列的通项公式；
②同一个数列的通项公式的形式不一定唯一。例如本题⑹，又如= 
=
；
③不是每个数列都有通项公式。如由
的不足近似值组成的数列1，1.4，1.41，1.414，…….
16．答案：（1）
，
故猜想数列的通项公式为：
；
（2）
.
17．解：由已知，得
因此
，由于不适合此等式，故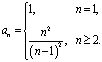
⑴
； ⑵令
，解方程得
，即
是该数列的第16项；
⑶∵
， ∴
.
18．解：⑴∵，又，
∴
令
，则
，∴
，
注意到，因此＝
， 
,
, ∴
即为数列的通项公式；
另解：由已知得
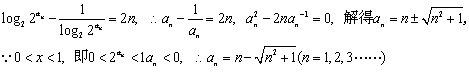
⑵
，可知数列
是递增数列.
说明：数列是一类特殊的函数，判定数列的单调性与判定函数的单调性的方法是相同的，只需比较an+1与an的大小。
19．解：⑴
，
；
⑵根据⑴猜想的一个通项公式为
.
20．分析：对任意的n都有
即指数列是单调递增的，可直接代入求
的取值范围.⑴解：
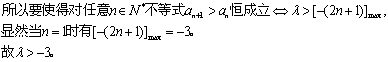
⑵由题意知：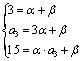
，解得
。
说明：⑴
；
⑵采用了“待定系数法”。