高一数学竞赛试题2
一、选择题：本大题共12小题；每小题6分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．请把符合题目要求的选项的字母填入答题卡中．
1．集合
中所有元素之和为
（A）－6 （B）－5 （C）5 （D）6
2．设全集
，
，
，则(
I
(I
（A）Ø （B）{1，2} （C）{1，2，5} （D） I
3．已知
、
为两个命题，则“或真”是“且真”的
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）既不充分也不必要条件
4．已知函数
=
在区间
上是增函数，则b满足的条件是
（A）
（B）
（C）
（D）与c的取值有关
5．函数
的反函数是
（A）
（B）
（C）
（D）
6．已知
则U的值域是（ ）
（A）[0，20] （B）[
，
（C）
（D）
7．在对数式
中，实数
的取值范围是
（A）
（B）
（C）
（D）
8．已知等差数列
满足
，则有
（A）
（B）
（C）
（D）
9．已知等差数列{an}的公差d＝
，a1＋a3＋a5＋a7＋a9＋…＋a95＋a97＋a99=60，
则a2＋a4＋a6＋a8＋a10＋…＋a96＋a98＋a100等于
（A）80 （B）85 （C）95 （D）110
10．方程
有实根，且2、
、
为等差数列的前三项．则该等差数列公差
的取值范围为
（A）
（B）
（C）
（D）
二、填空题：本大题共4小题；每小题4分，共16分．把答案填在题中横线上．
11．不等式
的解集是
．
12．在数列｛an｝中，an＝
，其中a、b、c均为正常数，则这个数列的单调性是
.
13．从集合
到集合
的映射的个数为
．
14．已知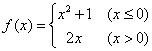
，若f(x)=10,则x＝
.
高一数学竞赛试题2
一、选择题
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
二、填空题
11、 ； 12、 ； 13、 ； 14、 .
三、解答题：本大题共6小题共74分．解答应写出文字说明．证明过程或演算步骤．
15、 (本小题满分12分)
解不等式：0≤
．
16、（本小题满分12分）
已知全集
，集合
，
，
，求实数a的取值范围：
（1）使
；
（2）使C
U A∩U B.
17、（本小题满分12分）
某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：
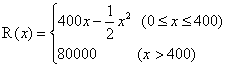，其中
是仪器的月产量．
（1）将利润表示为月产量的函数；
（2）当月产量为何值时，公司获利润最大？最大利润为多少元？
18、 (本小题满分12分)
函数对任意的m，n∈R都有
，且当x＞0时，
.
（1）求证：在R上是增函数；
（2）若
，解不等式
.
19、（本小题满分12分）
等差数列的公差是负数，且
．
（1）求
；
（2）问2003是否是数列
中的项，如果是，是第几项？如果不是，请说明理由．
20、（本小题满分14分）
已知数列中， 
，
，
.
（1）设
，求证：
是个等差数列，
（2）求数列的通项公式．
高一数学竞赛试题2
一、选择题：本大题共12小题；每小题6分，共60分．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | B | A | C | D | C | C | B | D |
二、填空题：本大题共4小题；每小题4分，共16分．
11．
12．单调递增 13．27 14．－3 或5
三、解答题：
15、解：原不等式等价于不等式组
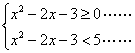………………………………2分
由①得
≥0,
∴①的解集是
；………………………………………………………………6分
由②得
，即
，
∴②的解集是
.…………………………………………………………………10分
∴原不等式的解集是
．…………………………………………12分
16、解：
，
或
……………………………………2分
（1）
，又
＜0，
即
且，
∴ 
，即
由此得≥1且
≤4，∴ 
；…………… 4分
又
时，C=Φ，满足题设，
∴ 使成立时a的取值范围是[1，2]∪{0}.………………………………………6分
（2）∵UA∩UB＝U(A∪B)＝
≤≤
，且CU A∩U B，由此得
.…………………………………………………………10分
∴ 使CU A∩U B成立时， a的取值范围是（－2，－
）.……………………… 12分
17、解：（1）依题意，总成本应为20000＋100x，从而
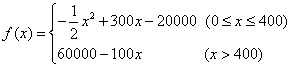…………………………………………6分
（2）当0≤≤400时，
∴当x=300时，有最大值25000；……………………………………………………8分
当x>400时，
是减函数，
∴
．
∴当x=300时，的最大值为25000．………………………………………………11分
答：每月生产300台仪器时，利润最大，最大利润为25000元．………………………12分
18、证明：（1）设x1，x2∈R，且x1＜x2，则x2－x1＞0，∴f(x2－x1)＞1.………………… 2分
而
∴是R上的增函数；…………………………………………………………………… 6分
解：（2）f(3)=f(2+1)=f(2)+f(1)－1=f(1+1)+f(1)－1=f(1)+f(1)－1+f(1)－1=3f(1)－2.
∵ ，即3f(1)－2＝4，∴ f(1)＝2……………………………………………………8分
∴不等式即为
，
又
是R上的增函数，∴
………………………………………………10分
解得：－3＜a＜2.
∴ 不等式的解集为{x－3<a<2}.………………………………………………………………12分
19、解：（1）由
得，
，
是方程
的两个根，
又∵等差数列的公差是负数，∴
∴
，公差
，………………………………………………4分
∵
，∴
，…………………………………………………………………5分
从而
；…………………………………………………6分
（2）由题意可知
……………………………9分
假设2003是数列
中的项，
当
时，
＝14－3n＝2003，n＜0，不合题意，
当n＞4时，＝3n－14＝2003，解得n＝
N*，
综上可知，2003不是数列中的项………………………………………………………12分
20、证明：(1) 已知.
两边同除以2n+1，得
……………………………………………3分
由于，即
，
∴ 
，……………………………………………………………………6分
故数列为等差数列. ………………………………………………………………………8分
（2）∵，
由（1）可知
＝……＝
＝
，…………………………………10分
∴是以为公差的等差数列,且
,
∴
.…………………………………………………………12分
又，
故：
＝
.……………………………………………………………14分