高一数学期末考试试题3
（满分：100分，时量：120分钟） 命题：李水平
一、选择题（共10小题，每小题3分，共30分）
1．设A={(x，y) y=－4x+6}，B={(x，y) y=5x－3}，则A∩B= ( )
（A）{1，2} （B）{(1，2)} （C）{x=1，y=2} （D）(1，2)
2．设全集U={1，2，3，4，5}，集合M={1，2，3}，N={2，3，5}，则
=( )
（A）Φ （B） {2，3} （C） {4} （D） {1，5}
3．下列函数中，是奇函数，又在定义域内为减函数的是 （ ）
（A） 
（B）
（C） y=－x 3
（D） 
4．随着计算机技术的不断发展，电脑的性能越来越好，而价格又在不断降低，若每隔两年电脑的价格降低三分之一，则现在价格为8100元的电脑在6年后的价格可降为 ( )
（A） 300元 （B） 2400元 （C） 2700元 （D） 3600元
5．已知映射
，使集合N中的元素y=x 2
与集合M中元素 x对应，要使映射为一一映射，则M、N可以为
( )
（A） M=R，N=R （B） M=R，N={y y≥0}
（C）M={x x≥0}，N=R （D）M={X x≤0}，N={y y≥0}
6．把函数
的图象经过下面一种变换可以得到函数y=2 x的图象，则这种变换是将的图象上的所有的点
( )
（A）向左平移2个单位 （B）向右平移2个单位
（C）向上平移2个单位 （D）向下平移2个单位
7．已知a>0，且a≠1，则下述结论正确的是 ( )
（A）
（B）
（C） 
（D）
8．命题“若x 2+y 2=0，则x、y全为0”的逆否命题是 ( )
（A） 若x、y全为0，则 x 2+y 2≠0 （B）若x、y不全为0，则 x 2+y 2=0
（C） 若x、y全不为0，则 x 2+y 2≠0 （D）若x、y不全为0，则 x 2+y 2≠0
9．已知函数f(x) 满足 f( x+4 )=x
3+2，则
等于
( )
（A） 
（B）
－1
（C） 
（D） 3
10．给出四个命题： （1） 2≤3 ； （2）如果m≥0, 则方程 x 2+x－m=0有实根；
（3） x 2 =y 2 Þ x = y ；（4）“a>b” 是 “a+c>b+c”的充要条件，其中正确的命题的个数有
（A） 1个 （B）2个 （C） 3个 （D） 4个 ( )
二、填空题（共5小题，每小题4分，共20分）
11．计算
=
12．已知数列{ a n }满足 a 1=1，以后各项由公式
给出，则 a 3 =
13．已知a<0且方程 ax 2+bx+c=0的两根为 x 1=1，x 2=2，则不等式 ax 2+bx+c>0 的解集为
14．我国2000年底的人口总数为M，要实现到2010年底我国人口总数不超过N（其中M<N），则人口的年平均自然增长率p的最大值是
15．给定集合A、B，定义一种新运算： A*B={ x x∈A或x∈B，但
}，又已知
A={0，1，2，}，B={1，2，3}，用列举法写出A*B=
三、解答题（共5小题，共计50分，每小题要有必要的解题过程）
16．（8分）成等比数列的三个数的乘积为64，并且这三个数分别减去1，2，5后又成等差数列，求这三个数
17．（10分）已知函数f ( x )=x 2+ax+b
（1）若对任意的实数x都有f (1+x)=f (1－x) 成立，求实数 a的值；
（2）若f (x)为偶函数，求实数a的值；
（3）若f (x)在[ 1，+∞)内递增，求实数a的范围。
18．已知一个等差数列{ a n }，S n为其前项的和，又知 S 10=110,S 20=420。
（1）求数列的通项公式 a n ； （2）求 S 30=?
19．某网民用电脑上因特网有两种方案可选：一是在家里上网，费用分为通讯费（即电话费）与网络维护费两部分。现有政策规定：通讯费为0.02元/分钟，但每月30元封顶（即超过30元则只需交30元），网络维护费1元/分钟，但每月上网不超过10小时则要交10元；二是到附近网吧上网，价格为1.5元/小时。
（1）将该网民在某月内在家上网的费用y（元）表示为时间t（小时）的函数；
（2）试确定在何种情况下，该网民在家上网更便宜？
20．已知函数
（1）求函数f ( x )的值域；
（2）求函数f ( x )的反函数
；
（3）证明：在(2，+∞)上为减函数。
高一数学参考答案及评分标准
一、BCDDB，CDADD
二、11 2 ；12 
； 13 {x 1<x<2 }（注：没有写成集合不给分）； 14 
－1 ；
15 A*B={0,3}
16．设所求的三个数为
, a ，aq （1分）则由题可知：·a·aq=a 3=64
Þ a=4,(3分）
于是由
－1，2，4q－5成等差数列 Þ(－1)+(4q－5)=4 Þ 2q 2－5q+2=0 Þ q=2或q=
,（6分） 代入得所求三个数为2，4，8或8，4，2（8分，只写一个结果扣1分）
17．（1） a=－2 (本小问4分）；（2） a=0 (本小问3分）；（3）a ≥－2 (本小问3分，但求出a=－2只给1分）
18.（1）设该数列的首项为a 1，公差为d,则有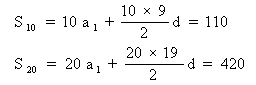
(3分）
解得 a 1=2，d=2 所以 a n=2n (6分）
（2）
由上可知 
=…=930
（10分）
19．（1）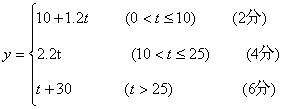
(2)上网时间超过60小时则在家上网便宜。（10分）（没有过程适当扣分）
20．(1) y≠2 (3分) (2) 
(6分）
（3）（本小问6分）不用定义证明的不给分，用定义证明f(x)的单调性的给分不超过2分.