高一数学期末试卷A
一、选择题(本题共12小题,每小题3分,满分36分,四个选项中只有一项是正确的。请将正确答案填入答卷纸上相应的位置)
1.若![]() ,
,![]() ,则下列各式中成立的是
,则下列各式中成立的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知向量![]() 都是非零向量,且
都是非零向量,且![]() 不共线,若
不共线,若![]() ,则
,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.函数![]() 的单调递增区间为
的单调递增区间为
A.![]()
![]() B.
B.![]()
![]()
C.![]()
![]() D.
D.![]()
![]()
4.若向量![]() ,
,![]() ,
,![]() 。则
。则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设![]() 为正六边形
为正六边形![]() 的中心,下列等式中成立的是
的中心,下列等式中成立的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.图象关于直线![]() 对称,且最小正周期为
对称,且最小正周期为![]() 的函数为
的函数为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.已知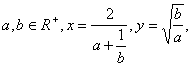 则
则![]() 与
与![]() 的关系为
的关系为
A.![]() B.
B.![]() C.
C.
![]() D.不确定
D.不确定
8.函数![]() 的图象按
的图象按![]() 平移以后得到的图象的解析式为
平移以后得到的图象的解析式为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.下列真命题的个数为
①![]() 取最小值时
取最小值时![]()
②![]() 则
则![]() 的最大值为1
的最大值为1
③![]() 的最小值为2
的最小值为2
④![]() 则
则![]() 的最大值为2
的最大值为2
A. 0 B. 1 C. 2 D. 3
10.已知![]() 中,
中,![]() ,则
,则![]() 为
为
A.等腰直角三角形 B.等腰三角形
C.直角三角形 D.既不是等腰三角形,也不是直角三角形
11.在![]() 中,若
中,若![]() ,
,![]() 为钝角,则
为钝角,则![]() 的取值范围为
的取值范围为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 且
且![]()
12.已知![]() 中,角
中,角![]() 所对的边为
所对的边为 ![]() ,若
,若![]() 且
且![]() ,则使此三角形有两组解的边
,则使此三角形有两组解的边![]() 的取值范围为
的取值范围为
A. ![]() B.
B.
![]() C.
C.![]() D.
D.
![]()
二、填空题(本题共4个小题,每小题4分,满分16分,请将正确答案填在答卷纸相应的横线上)
13.已知![]() ,则
,则![]() 。
。
14.已知点![]() 和
和![]() ,且点
,且点![]() 分有向线段
分有向线段![]() 的比为
的比为![]() 。则
。则![]() ,
,![]() 。
。
15.若![]() 为任意向量,给出下列各式:
为任意向量,给出下列各式:
①![]() ②
②![]()
③若![]() ,则
,则![]() 或
或![]() ④
④![]()
一定成立的是 。
16.把长为12cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是
班级 姓名 学号 得分
一、 选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题
13. 14. 15 16.
三、解答题(本题共6小题,第17题6分,第18题6分,第19题6分,第20题10分,第21题8分,第22题12分,满分48分。解题应写出文字说明和必要的解题步骤)
17.已知![]() (1)若
(1)若![]() 与
与![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() 与
与![]() 共线,求
共线,求![]() 的值。
的值。
18. 已知![]() ,求证:
,求证: ![]()
19.在![]() 中,
中,![]() 分别是角
分别是角![]() 所对的边,若
所对的边,若![]() 且
且![]() 。
。
⑴求证:![]() ; ⑵求角
; ⑵求角![]() 的值。
的值。
20.已知向量![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 两两的夹角都是
两两的夹角都是![]() .
.
求(1)![]() ;
;
(2)![]() ;
;
(3)![]() 与
与![]() 所成的夹角。
所成的夹角。
21.已知函数![]() ,
,
求(1)![]() 可以由
可以由![]() 经过怎样的变换得到?
经过怎样的变换得到?
(2)当![]() ,求函数
,求函数![]() 的最大值和最小值。
的最大值和最小值。
22.如图,用两根绳子挂着一个物体,物体受到的重力为1![]() 。
。
(1)当两条绳子长度相等且所夹角![]() 时,求每条绳子所受到的拉力的大小
时,求每条绳子所受到的拉力的大小
(2)已知两根绳子长度相等,设绳子受到的拉力为![]() ,求证:
,求证:![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (3)若将两条绳子换成两根夹角为
(3)若将两条绳子换成两根夹角为![]() 的细杆
的细杆![]() (细杆重量忽略不计),细杆所受到的拉力分别为
(细杆重量忽略不计),细杆所受到的拉力分别为![]() ,求
,求![]() 的最大值,并说明何时达到最大值。
的最大值,并说明何时达到最大值。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
班级 姓名 学号 得分
一、 选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | C | B | A | C | B | B | C | B | B | D | C |
二、填空题
13. ![]() 或
或![]() 14.
14. ![]() 15.
①②④ 16。
15.
①②④ 16。![]()
三、解答题(本题共6小题,第17题6分,第18题6分,第19题6分,第20题10分,第21题8分,第22题12分,满分48分。解题应写出文字说明和必要的解题步骤)
17.已知![]() (1)若
(1)若![]() 与
与![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() 与
与![]() 共线,求
共线,求![]() 的值。
的值。
解:(1)由![]() 得
得![]()
![]()
(2)由![]() 得
得![]() ,
,![]()
![]()
18. 已知![]() ,求证:
,求证: ![]()
证明1 由![]()
![]()
证明2 ![]()
![]()
19.在![]() 中,
中,![]() 分别是角
分别是角![]() 所对的边,若
所对的边,若![]() 且
且![]() .
.
⑴求证:![]() ; ⑵求角
; ⑵求角![]() 的值。
的值。
解:(1)![]()
![]()
![]()
![]() ,
,![]() ,所以
,所以![]() 。
。
(2)由![]() 得
得![]() ,
,
又![]()
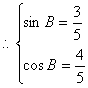
![]()
20.已知向量![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 两两的夹角都是
两两的夹角都是![]() .
.
求(1)![]() ;
;
(2)![]() ;
;
(3)![]() 与
与![]() 所成的夹角。
所成的夹角。
解: (1)![]()
(2)![]()
![]()
(3)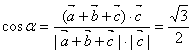 ,
,![]()
21.已知函数![]() ,
,
求(1)![]() 可以由
可以由![]() 经过怎样的变换得到?
经过怎样的变换得到?
(2)当![]() ,求函数
,求函数![]() 的最大值和最小值。
的最大值和最小值。
解(1)化简得![]() 。可以将
。可以将![]()
向右平移![]() 个单位,横坐标缩小到原来的
个单位,横坐标缩小到原来的![]()
(2)![]() 时,
时,![]()
![]() 时,
时,![]()
22.如图,用两根绳子挂着一个物体,物体受到重力为1![]() 。
。
(1)当两条绳子长度相等且所夹角![]() 时,求每条绳子所受到的拉力的大小
时,求每条绳子所受到的拉力的大小
(2)已知两根绳子长度相等,设绳子受到的拉力为![]() ,求证:
,求证:![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (3)若将两条绳子换成两根夹角为
(3)若将两条绳子换成两根夹角为![]() 的细杆
的细杆![]() (细杆重量忽略不计),细杆所受到的拉力分别为
(细杆重量忽略不计),细杆所受到的拉力分别为![]() ,求
,求![]() 的最大值,并说明何时达到最大值。
的最大值,并说明何时达到最大值。
解:(1)拉力为![]()
![]() (2)
(2)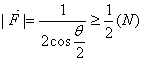
![]()
![]()
(3)设长度为![]() 的细杆与水平方向所夹的锐角为
的细杆与水平方向所夹的锐角为![]()
由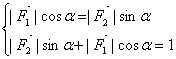
得![]()
![]()
![]()
此时![]() 且
且![]() ,最大值为
,最大值为![]() 。
。