高一数学期末综合测试（2）月考3

高一语数英期末检测—数学卷

一、选择题：

1.已知角α的终边经过点P(2a,-4a)(a＜0)，则下列结论不正确的是　　　[　 ]

  A.sinα=　 B.cosα=　 C.tanα=-2　　　 D.cotα=-

2.在△ABC中，已知三边满足：(a+b+c)(a+b-c)=3ab,则角C等于　　　　 [　 ]

  A.150⁰　　　 　 B.30⁰　　　　  C.45⁰　　　　　  D.60⁰

3.若函数f(x)定义域为[0,1]，则f(cosx)的定义域为　　　　　　　　　 [　 ]

  A.[0,1]　　　　 B.[-,]　  C.[2kπ-,2kπ+](k∈Z) D.R

4.已知三点A(-5,6),B(2,3),C(-,4)，则点C分所成的定比λ为　　 [　 ]

  A.-2　　　　　  B.1　　　　　 C.2　　　　　　  D.-1

5.已知sin(+α)=-,α∈(π,),则cos(-α)的值为　　　　　  [　 ]

  A.　　　 B.　　 C.- 　　　D.

6.将函数y=的图象按平移，平移后的函数解析式为y=,则=  [　 ]

  A.(-2,1)　　　　 B.(2,-1)　　  C.(1,-1)　　　  D.(-1,1)

7.使函数y=sin(2x+φ)+cos(2x+φ)为奇函数，且在[0,]上是

  减函数的φ的一个值是　　　　　　　　　　　　　　　　　　　　　  [　 ]

  A.　　　　　 B.　　　　  C.　　　　　 D.

8.在　 ABCD中，+++++=　　　　　　　　  　　　[　 ]

  A.　　　　　  B.2　　　　C.　　　　  D.2

9.已知f(x)=sin(x+),g(x)=cos(x-),则f(x)的图象　　　　　　　  [　 ]

  A.与g(x)图象相同　　　　　　　 B.与g(x)图象关于y轴对称

  C.向左平移个单位得到g(x)图象 D.向右平移个单位得到g(x)图象

10.△ABC的边长为AB=6，BC=3，AC=5，则·=　　　　　　　　 [　 ]

　 A.10　　　　 　B.-12　　　　　C.-10　　　　 D.20

11.把函数y=sin(-3x)的周期扩大为原来的2倍，再将所得到的函数的

　 图象向右平移个单位，则所得到的图象的函数解析式为　　　　  [　 ]

　 A.y=sin(-)　　　　　　  B.y=cos

　 C.y=sin(-)　　　　　　  D.y=sin(-6x)

12.已知sinα=sin²α+sin²β，则函数y=sin²α+sin²β的值域是　　 [　 ]

　 A.(-,)　　 B.[0,]　 　　C.[0,]　　　 D.[0,]

二、填空题：

13.已知=(1,0),=(1,1),=(-1,0),且=λ+μ,

　 则实数λ=　　　　,μ=　　　　；

14.某人向正东方向走xkm后，他向右转150⁰，然后朝新方向走3km，

　 结果他离开出发点恰好km，则x=　　　 ；

15.y=sinx(sinx+cosx)的最小正周期是　　　 ；

16.设、、是任意非零共面向量，且相互不共线，那么

　 ①⊥+=-；　　②=（+）⊥（-）；

　 ③（·）·=（·）·； ④16²-25²=（4-5）²；

　 ⑤若==且三个向量两两所夹的角相等，则++=.

　 其中假命题的序号是　　　　 .

高一语数英期末检测—数学卷答卷（1）

一、选择题：（5′×12）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题：（5′×4）

13.　　　 ，　　　 ；　 14.　　　　　　  ；  15.　　　 ；　16.　　　.

三、解答题：

17.（10′）化简：

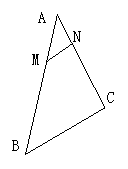18.（10′）如图，=，=，求证：=.

19.（12′）已知α、β为锐角，且3sin²α+2sin²β=1，3sin2α-2sin2β=0,

　　求证：α+2β=.

20.（12′）已知=4，=3，（2-3）·（2+）=61.

　　①求与的夹角；　②求+和-.

数学卷答卷（2）

21.（12′）正方形场地ABCD边长为200m，在A附近已先占用以A为圆心以100m

　　为半径的圆的场地，今要在余下场地上建一矩形楼房，使矩形两边分别在BC

　　和CD上，（如图）.问：这幢楼房的最大占地面积是多少m²？

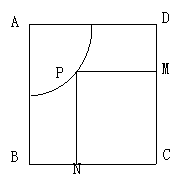22.（14′），是直角坐标系中x轴和y轴正方向上的单位向量，

　 设=(m+1)-3, =+(m-1),

　 ①若(+)⊥(-),求m；

　 ②若m=-2时，求 与的夹角θ；

　 ③是否存在实数m，使∥，若有则求出m，没有则说明理由.