高一数学期末综合测试（3）
一、选择题
1、在等边△ABC中，
+
= A、
B、
C、
D、以上均不对 [ ]
2、下列函数中，以为π最小正周期的偶函数，且在（0，
）内递增的是
[ ]
A、y=sinx B、y=sinx C、y=cosx D、y=cosx
3、已知cos（α- 
）=
，则sin2α的值为 A、
B、- C、
D、- [ ]
4、若
=（1，1）
=（1，-1）
=（-1，2），则= +
[ ]
A、
B、
C、
D、
5、，为非零向量，且=，若k+与k-相互垂直，则实数k的可能值为 [ ]
A、1 B、2 C、0 D、任意实数
6、△ABC中，若C=900，则sin2A= A、
B、
C、
D、
[ ]
7、△ABC中，若b=2a sinB，则A= 0A、30 B、60 C、30或150 D、60或120 [ ]
8、若
·=·，且≠则
[ ]
A、= B、=λ（λ∈R） C、⊥ D、、在方向上的投影相等
9、=（cosα，sinα）=（cosβ，sinβ）则有
[ ]
A、⊥ B、∥ C、（+）⊥（-） D、与的夹角为α-β
10、△ABC中，
=，=，则·<0 是△ABC为钝角三角形的 [ ]
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、非充分非必要条件
二、填空题
11、函数
的定义域为
12.
13、已知·=2，=2，=
，则与的夹角
14、若P在直线P1P2上，且P1P2=2PP1，则点P分
所成的比λ=
三、解答题
15、已知+=（2，- 8），-=（-8，16），求与的夹角
16、△ABC中，若sinB=sinAcosC，且△ABC最大边长为12，最小角的正弦为
，
（1）判断△ABC的形状 （2）求△ABC的面积
17、△ABC中，已知=，=，求证：S△ABC=
18、已知y=sinx+sin2x-cosx（0≤x≤π）（1）求sinx-cosx的取值范围 （2）求这个函数值域
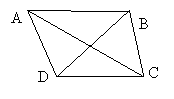19、在四边形ABCD中，CD=，∠ACD=300，∠ADC=1200，∠BDC=450，∠BCD=750，
求AB的长.