高一数学第二学期期中考试试题1
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,
共150分。考试时间120分钟。
第I卷(选择题60分)
一、 选择题:本在题共12个小题,每小题5分,满分60分。
在每小题的四个选项中,只有一项符合要求。
(1)下列命题中的真命题是
(A)终边相同的角必相等
(B)第二象限的角比第一象限的角大
(C)三角形的内角必是第一象限或第二象限的角
(D)角![]() 的终边在X轴上时,角
的终边在X轴上时,角![]() 的正弦线、正切线都变成一个点
的正弦线、正切线都变成一个点
(2)![]() 的值为
的值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(3)函数![]() 的值域是
的值域是
(A){3} (B){3,-1}
(C){3,1,-1} (D){3,1,-1,-3}
(4)下列函数中,周期为![]() 的偶函数是
的偶函数是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(5)若![]() 则
则![]() 的值为
的值为
(A)![]() (B)1 (C)
(B)1 (C)![]() (D)0
(D)0
(6)下列不等式中,正确的是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(7)当![]() 时,函数
时,函数![]() 的
的
(A)最大值是![]() ,最小值是
,最小值是![]() (B)最大值是
(B)最大值是![]() ,最小值是1
,最小值是1
(C)最大值是2,最小值是1 (D)最大值是2,最小值是![]()
(8)若![]() ,则
,则![]() 的值等于
的值等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(9)已知![]() ,则tan
,则tan![]() 的值是
的值是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(10)已知点![]() ,
,![]() 在第二象限,则
在第二象限,则![]() 的一个变化区间是
的一个变化区间是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(11)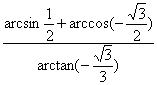 的值等于
的值等于
(A)![]() (B)6 (C)
(B)6 (C)![]() (D)
(D)![]()
(12)关于函数![]()
![]() ,有下列命题:
,有下列命题:
①![]()
②![]()
③![]()
④![]()
其中正确的例题的序号是
(A)①③④ (B)③④ (C)①④ (D)①③
第II卷(非选择题 共90分)
二、 填空题:本大题共4小题,每小题4分,共16分。把答案
填在题中横线上。
(13)若![]() 是第三象限角,则
是第三象限角,则![]() 是第__________象限角.
是第__________象限角.
(14)若扇形的周长是8cm,面积4cm2,则扇形的圆心角为_________rad.
(15)![]() ____________.
____________.
(16)化简![]() 的结果_________
的结果_________
三、解答题:本大题共6小题,共74分。解答应写出文字说明,
证明过程或演算步骤。
(17)(本小题10分)化简 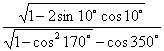
(18)(本小题10分)![]()
![]()
(19)(本小题12分)
已知![]()
求证:![]()
(20)(本小题14分)已知函数![]()
(1)当函数y取得最大值时,求自变量x的集合;
(2)该函数的图象可由y=sinx(x![]() R)的图象经过怎样的平移和
R)的图象经过怎样的平移和
伸缩变换得到?
(21)(本小题14分)地面上有两座塔AB、CD,相距120米,一人分别在两塔底部测得一塔顶仰角为另一塔顶仰角的2倍,在两塔底连线的中点O测得两塔顶的仰角互为余角,求两座塔的高度
|
A O C |
(22)(本大题14分)![]() ,其中
,其中![]() 、
、![]() 是常数,且满足
是常数,且满足![]() ,是否存在这样的
,是否存在这样的![]() 、
、![]() ,使
,使![]() 是与
是与![]() 无关的定值。若存在,求出
无关的定值。若存在,求出![]() 的值;若不存在,说明理由。
的值;若不存在,说明理由。
第二学期期中高一数学试题1参考答案与评分标准
一、选择题:共12小题,每小题5分,共60分
DCBBA BCDAC AD
二、填空题:共4小题,每小题4分,共16分
(13)一 (14)2
(15)![]() (16)
(16)![]()
三、解答题:共6小题,共74分
(17)(满分10分)
原式=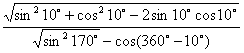 4分
4分
![]() 6分
6分
![]()
![]() 10分
10分
(18)(满分10分)
![]()
![]()
![]() 3分
3分
![]() 7分
7分
![]() 10分
10分
(19)(满分12分)
因为![]()
所以![]() 4分
4分
![]()
![]()
![]() 8分
8分
![]()
![]() 10分
10分
![]() 即
即![]() 12分
12分
(20)(满分14分)
![]()
![]() 2分
2分
当y取得最大值时,必需且只需
![]()
当y取得最大值时,x的集合为
![]() 6分
6分
(2)将函数y=sinx的图象依次进行如下变换:
![]()
![]()
![]() 10分
10分
![]()
![]()
![]()
![]() 14分
14分
|
B
A O C |
(21)(满分14分)
连结BO、OD、 AD、 BC,
设两塔AB、CD的高分别为x米,y米,
![]() ,
,
![]()
![]()
![]()
![]() (
1 ) 5分
(
1 ) 5分
![]() ,
,![]() ,
,
![]() (2)
10分
(2)
10分
由(1)(2)式解得: x = 40(米), y = 90(米)
答:两座塔的高分别为40米、90米。 14分
(22)(满分14分)
假设存在这样的![]() ,使
,使![]() 是与
是与![]() 无关的定值,
无关的定值,
可取![]() 的值分别为
的值分别为![]() ,则
,则
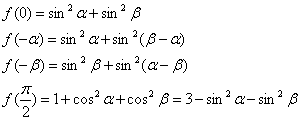
![]()
![]() 6分
6分
![]()
![]()
![]() ,
,![]() 10分
10分
此时,![]()
![]()
![]()
![]()
![]() 14分
14分