高一数学第一次月考试题
第Ⅰ卷（选择题 共60分）
一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
（1）已知集合
，那么集合
为
(A) x = 3，y = –1 (B) {3，–1} (C) (3，–1) (D) {(3，–1)}
（2）不等式
的解集为
(A)
(B)
(C)
(D)
（3）若
、
是两个简单命题，且“或”的否定是真命题，则必有
(A) 真真
(B) 假假
(C) 真假
(D) 假真
（4）“
”是“函数
的最小正周期为
”的
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既非充分又非必要条件
（5）下列各项中能表示同一函数的是
(A)
与
(B)
与
(C)
与
(D)
与
（6）已知
，则
(A)
(B)
(C)
(D) 
（7）若
区间
上
(A)单调递增 (B)单调递减 (C)先增后减 (D)先减后增
（8）设
是
上的奇函数，
，当
时
，则
等于
(A)0.5 (B)-0.5 (C)1.5 (D)-1.5
（9）已知二次函数
满足
，且有两个实根
，
，则
=
(A)0 (B)3 (C)6 (D)不确定
（10）函数
的增区间是
(A)
(B)
(C)
(D)
（11）若函数
的值域是
，则实数
的取值范围是
(A)
(B)
(C)
或
(D)
或
（12）已知函数
，则它的反函数
的图象是
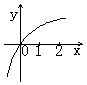
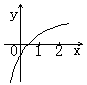
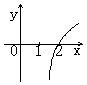
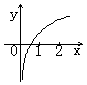
(A) (B) (C) (D)
第Ⅱ卷（非选择题 共90分）
二．填空题:本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
（13）函数
的反函数为
．
（14）函数f (x) 对任何x
R+ 恒有f (x1·x2) = f (x1) + f (x2)，已知f (8) = 3，则f (
) =_____．
（15）已知函数
在区间
上是增函数，则
的取值范围是
．
（16）如果函数
的定义域为，则实数的范围是
．
三．解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
（17）（本小题满分12分）
求不等式
。
（18）（本小题满分12分）
设集合
，
，若
，求实数的取值范围。
（19）（文科）（本小题满分12分）
已知
，
，求
的值。
（理科）（本小题满分12分）
求函数
的值域。
（20）（文科）（本小题满分12分）
求函数的值域。
（理科）（本小题满分12分）
若奇函数在定义域
上是减函数，求：
① 函数
及
的定义域；
② 满足
的实数的取值范围。
（21）（文科）（本小题满分12分）
若奇函数在定义域
上是减函数，求：
① 函数及的定义域；
② 满足的实数的取值范围。
（理科）（本小题满分12分）
已知
，若
在区间
上的最大值为
，最小值为
，令
。
① 求
的解析式；
② 判断的单调性，并求出的最小值。
（22）（文科）（本小题满分14分）
已知，若在区间上的最大值为，最小值为，令。
① 求的解析式；
② 判断的单调性，并求出的最小值。
（理科）（本小题满分14分）
设f (x)
= 2(log2x)2 + 2alog2
+ b，已知x =
时，f (x) 有最小值 –8．
① 求a与b的值； ② 在 ① 的条件下，求f (x) > 0的解集A；
③ 集合B ={x x –t ≤，xR}，且A
B =
，求实数t 的取值范围．
（附加题，满分10分，不计入总分）
已知二次函数f (x) = ax2 +bx + c (a、b、c均为实数)，且同时满足下列条件：
① f (–1) = 0；② 对任意实数x，都有f (x) –x≥0；③ 当x(0，2)时，有f (x)≤(
)
．
（1） 求f (1)； （2） 求a、b、c 的值；
（3） 当x[–1，1] 时，函数g (x) = f (x) –mx (m是实数)是单调函数，求m 的取值范围．