高一数学第一学期教学质量检测试卷-高中一年级数学试题练习、期中期末试卷、测验题、复习资料-高中数学试卷-试卷下载

高一数学第一学期教学质量检测试卷

题号	1-12	13-16	17	18	19	20	21	22	总分
得分

注：所有计算问题均可使用计算器；本试卷满分150分，在120分钟内完成

一、选择题：（每题5分，共60分，将答案直接填在下表中）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

1、设集合M={x x<3，x∈R}，a=，下列选项正确的是

A、aM　　　　　B、{a}∈M　　　 C、aM　　　　　 D、{a}M　

2、设全集U={a，b，c，d，e}，集合M={ a，c，d}，N={b，d，e}，那么MC_UN是　　　　　　　　　　　　　　　　　　　　　　　　　

　　A、　　　　　　B、{d}　　　　　　C、{b，e} 　　　　D、{a，c}

3、下列解不等式的结果错误的是

A、x-3<0的解集为　　 B、≥0的解集是R

C、x²< 3x的解集是　　　　　 D、<0的解集是

4、“P且q为真命题”是“p或q为真命题”的什么条件

　　A、充分不必要条件　　　　　　　　　 B、必要不充分条件

　　C、充分必要条件　　　　　　　　　　 D、既不充分也不必要条件

5、已知集合A={0，4}，B={0，2}，下列从A到B的对应关系为f，x∈A，y∈B，不是映射的是

A、　　B、　C、　 D、

6、设x取实数，则f(x)与g(x)表示同一个函数的是

A、f(x)=x，　　　　　　　 B、，

　C、f(x)=1，g(x)=(x-1)⁰　　　　　　　　 D、，g(x)=x-3

7、已知偶函数f(x)在上单调递减，则f(1)和f(-10)的大小判断较准确的是

　　A、f(1)> f(-10)　　　B、f(1)<f(-10)　　 C、f(1)≥f(-10) 　　 D、f(1)≤f(-10)

8、已知f(x)=x²+1（x≥3），则f^-^-1(x)的值域是

A、[3，+∞）　　　 B、[0，+∞）　　　C、[1，+∞）　　　 D、（-∞，0]

9、函数y=(a²-1)^x在上是减函数，则a的取值范围是

A、a>1　　　　　 B、a>　　　 C、a>　　　　　D、1<a<

10、如右图，在直角坐标系的第一象限内，△AOB是边长为2

的等边三角形，设直线l：x = t（0≤t≤2）截这个三角形，

所得位于直线左侧的图形的面积为f(t)，则函数y=f(t)的

图象只可能是

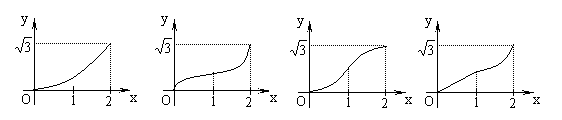　　　　　 A　　　　　　　　　 B　　　　　　　　 C　　　　　　　 D

11、数列1、3、6、10、…的一个通项公式是

　　A、a_n=n²-(n-1)　　　B、a_n=n²-1　　　　C、a_n=　　 D、a_n=

12、等差数列{a_n}中，a_m+n= α，a_m-n= β，则其公差d的值为

　　A、　　　　 B、　　　　 C、　　　　 D、

二、填空题：（每题4分，共16分，将答案直接填在下表中）

题号	13	14	15	16
答案

13、已知函数=3x-2，若=4，则a的值是___________.

14、f：A→B是从A到B的映射，其中集合A = B = {( x，y ) x，y∈R }，

．那么B中元素（－5，2）的原象是　　　　　　 .

15、已知函数=，则=_________.

16、有下列四个命题：

①空集是任何集合的真子集；

②命题“面积相等的三角形全等”的否命题；

③若命题p的逆命题是q，命题p的否命题是r，则q是r的逆否命题；

④2与8的等比中项是4 .

其中正确命题的序号是_______________. （把你认为正确命题的序号都填上）

三、解答题：（第17题16分、第18题10分，其它题各12分，共74分）

17、计算下列各式：

（1）-4×

（2）化简：

解：

18、解关于x的不等式：

解：

19、公差d不为零的等差数列{a_n}的第二、第三、第七项恰好构成等比数列，求这个等比数列的公比q .

解：

20、用长为 m的铁丝弯成下部为矩形，上部为半圆型的框架，若矩形的底边AB的长为 2x，求此框架围成的面积y与x的函数解析式，并写出它的定义域.

解：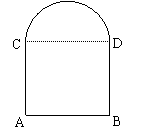

21、福兴公司从2002年起，每人的年工资已由三个项目组成并按下表规定实施

项　目	计　算　办　法
基本工资	2002年1万元，考虑物价因素，以后每年递增10%
住房补贴	按在公司工作年限计算：在公司工作第一年补3600元，以后每年比上年多500元（工作年限计算办法，如某职工1999年进公司，到2002年按4年计算）
医疗补贴	每年2400元，固定不变