高一数学第一学期期末考试卷3·
一、 选择题（每小题5分，共60分）
1. 下列说法正确的是（ ）
(A)
集合
用列举法表示是{0，1}
(B) 集合{a，b}与集合{b，a}表示不同的集合
(C) 0不是N集合的元素
(D)
不等式
的解集是
2.
已知U={1，2，3，4}，集合A={1，2，4}，则
（ ）
(A) {3，5} (B){0，3，5} (C){3} (D){0，5}
3.
不等式
的解集为（ ）
(A)
(B) 
(C) 
(D) 
4.
设
取实数，则
与
表示同一个函数的是（ ）
(A) 
，
(B)
，
(C)
，
(D)
，
5.
已知
，则
的值域是（ ）
(A) 
(B)
(C) 
(D)
6.
函数
在
上是减函数，则
的取值范围是（ ）
(A)
(B) 
(C) 
(D)
7.
已知数列
的前
项和
，则
的值是（ ）
(A)390 (B)397 (C)398 (D)400
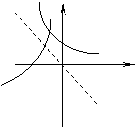
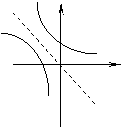
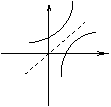
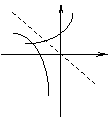
8.
已知
，函数
与
的图像只可能是（ ）
y
y
y
y
O x O x O x O x
(A) (B) (C) (D)
9.
是
成等比数列的（ ）
(A) 必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)什么条件也不是
10.
将函数
的图像向左平移2个单位后再向下平移2个单位，得到
的图像，函数的图像与的图像关于直线
对称，则的表达式为（ ）
(A)
(B) 
(C)
(D) 
11.
有下列四个命题：（1）“若
，则
”的逆命题；（2）“全等三角形的面积相等”的否命题；（3）“若
，则
有实根”；（4）“若
，则
”的逆否命题。
其中真命题的个数是（ ）
(A) 1 (B)2 (C) 3 (D) 4
12.
如果函数
在[1,2]上的最大值比最小值多2，则底数的值是（ ）
(A) 
(B) 
(C) 或
(D) 或2
二、填空题（每小题4分，共16分）
13.
集合
是单元素集，则
=___________________
14.
已知偶函数在上单调递减，则
和
的大小关系为___________________
15.
数列中，
，
且
，则
=___________________
16.
对于函数
，下列命题中，不正确的命题的序号是___________________
① 的图像关于原点对称；②在R上是增函数；
③
；
④
有最小值0
三、解答题（共74分）
17．（12分）设
，
，已知
，求的值。
18．（12分）已知点（1，2）既在函数
的图像上，又在它的反函数图像上，求，
的值。
19．（12分）计算下列各式：（1）
（2）
20．（共12分）已知为一次函数，且
成等比数列，又
，
（1）
求
的表达式；
（2）
当
时，求
的值。
21．（共12分）已知不等式
（1）
如果不等式的解集是
，求
的值；
（2）
如果不等式的解集是
，求的取值范围。
22．（共14分）已知函数
是奇函数，且
。
（1）
求函数的解析式；
（2）
指出函数的单调区间，并加以证明。
============================================================================================================================================
参考答案
选择题（每小题5分，共60分）
1~5 DCDBD 6~10 DBBBB 11~12 AC
填空题（每小题4分，共16分）
13． 
14. 
15. 29 16. ③
解答题（共74分）
17．解：∵，∴9
若
,则
此时
，
，这与矛盾；
若
,则
，当
时，
与集合中元素的互异性矛盾；当
时，
，
，符合题设条件。
故
18．解：由题设条件可得：点（1，2）和点（2，1）都在函数的图像上，故可得方程：
······①
及 
······②
解得
,
19．解：(1)原式=···=110；
（3）
原式=
=
=
20．解：（1）设所求的一次函数为
，（
）
由题设条件成等比数列，可得：
···①
又，得
···②
且题中，故由方程①,②联立解得
，
，∴
∴数列
的通项公式为
,易知是以
为首项，
为公差的等差数列，故其前项和
=
；
（2）
21．解：(1)根据二次函数与方程的关系，由题设条件得：
，且
，
为关于的方程
的两个实数根，据韦达定理有
，∴
(2)，且
，解得
22．解：(1)∵是奇函数，∴对定义域内的任意的，都有
，
即
，整理得：
∴
···①
又∵，∴
，解得
···②
∴所求解析式为
(2)由（1）可得
=
，函数的定义域为
，并且由于是奇函数，可先考查其在区间
上的单调性。
设
，则由于
=
···※
因此，当
时，
，从而得到
即
，
∴
是的增区间。
当
时，由上述※式可得，
∴是的减区间。
综上所述，增区间是
和；减区间是
和。