高一年级数学科
上学期期末试卷（B）
| 题序 | 1—12 | 13—16 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
| 得分 |
一、选择题（每小题给出的答案中，正确答案唯一，把正确答案的英文代号填入题后的（ ）内，每小题3分，本题36分）
1．设
是集合
到
的映射，下列命题中真命题的是…………（ ）
（A）中每一个元素在中必有象（B）中每一个元素在中必有原象
（C）中不同的元素必有不同的象（D）中每一个元素在中原象唯一
2.已知四组函数，每组有两个函数
①
②
③
④
其中表示同一函数的组别………………………………………………………（ ）
（A）仅有①（B）仅有②（C）仅有②④（D）有②③④
3.若奇函数
在区间
上是增函数，且有最大值为3，则在区间
上是………………………………………………………………………………（ ）
（A）增函数，最大值为-3（B）增函数，最小值为-3
（C）减函数，最大值为-3（D）减函数，最小值为-3
4.设：
3是1和5的等差中项，
4是2和5的等比中项，
则下列说法正确的是……………………………………………………………（ ）
（A）“非p”为真（B）“非q”为假（C）“p且q”为真（D）“p或q”为真
5.已知
则函数
的最小值是（ ）
（A）5（B）4（C）8（D）无最小值
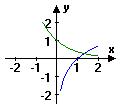
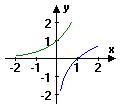
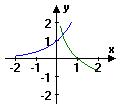
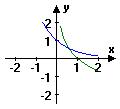
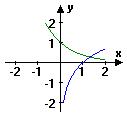
6.当
时，在同一坐标系中，函数
与
的图象是……（ ）
（A）
（B）
（C）
（D）
7.设
为等差数列，且
，
若
则
为……………………………………………………………………………（ ）
（A）16（B）18（C）20（D）22
8.已知数列和
都是等差数列，它们的前n项和分别为
和
并且
则
…………………………………………………………（ ）
（A）
（B）
（C）
（D）
9.数列满足
，且
则
………（ ）
（A）1（B）2（C）3（D）4
10.已知等比数列中，
则公比
……………………（ ）
（A）
（B）
（C）
（D）
11.已知等差数列中，
，等比数列中，
，是数列的前n项和，是数列的前n项的积，则……………………………（ ）
（A）
（B）
（C）
（D）
12. 
是
，
，
成等比数列的…………………………………（ ）条件
（A）充要（B）充分而不必要（C）必要而不充分（D）非充分非必要
二、填空题（每小题4分，共16分）
13.函数
的单调递增区间是
。
14.写出数列
的一个通项公式
。
15.
。
16.某工厂八年来某种产品总产量c随时间t（年）的函数关系如图：
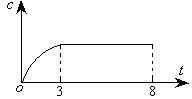①前3年中产量增长速度越来越慢；
②前3年中产量增长速度越来越快；
③第三年后，这种产品停止生产；
④第三年后，产品增长的速度保持稳定
其中说法正确的有 。
三、解答题（要求写出完整的解题过程，本题共48分）
17.（本小题6分）已知
，求（1）
（2）
18. （本小题8分）已知
的定义域为R，求实数
的取值范围，并求的值域。
19. （本小题8分）某商店积压了100件某商品。为让这批货尽快脱手，该商店采取如下方案：将价格提高到原价的2.5倍，再作三次降价处理。
第Ⅰ次降低30%，标出“亏本价”，
第Ⅱ次再降低30%，标出“破产价”，
第Ⅲ次又降低30%，标出“跳楼价”。
结果：第Ⅰ次降价处理仅售出5件；
第Ⅱ次降价处理售出40件；
第Ⅲ次降价处理，剩下商品被一抢而空。
问：1）“跳楼价”与原价之比为多少？
2）该商店按新销售方案，比较与按原价全部销售，哪一种方案盈利多？
20.（本小题10分）设
（1）判断f(x)的奇偶性，并予以证明；
（2）证明：在
上是增函数；
（3）判断在
上的单调性；
21. （本小题6分）已知数列满足
，
，
求的通项公式及前n项和
22. （本小题10分）已知数列的前n 项和
（1）求数列的通项公式并证明是个等差数列；
（2）问n取何值时，达到最大，最大值为多少；
（3）求数列
的前n项之和的表达式。