高一年级数学科下学期期中试卷(B)
(试卷Ⅰ)
一、选择题(每小题给出答案中,正确答案唯一,每小题3分,本题共36分)
1.若![]() 为第一象限角,则
为第一象限角,则![]() 是………………………………………………( )
是………………………………………………( )
(A)第一象限角(B)第二象限角(C)第三象限角(D)第四象限角
2.![]() 的值是…………………………………………………………………( )
的值是…………………………………………………………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.下列各式中正确的是 …………………………………………………………( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
4.函数![]() 的最小值是………………………………………( )
的最小值是………………………………………( )
(A)
![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.在![]() 中,
中,![]() ,则
,则![]() 的值是………………( )(A)
的值是………………( )(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.函数![]() 是…………………………………………………( )
是…………………………………………………( )
(A)周期为![]() 的偶函数(B)周期
的偶函数(B)周期![]() 为的奇函数
为的奇函数
(C)周期为![]() 的偶函数(D)周期为
的偶函数(D)周期为![]() 的奇函数
的奇函数
7. 使函数![]() 与
与![]() 都是减函数的一个区间是……………………( )
都是减函数的一个区间是……………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8. 等腰三角形的底角余弦值为![]() ,则顶角的正弦值……………………………( )(A)
,则顶角的正弦值……………………………( )(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
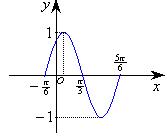 9. 若
9. 若![]() 的图象如下图所示,则
的图象如下图所示,则![]() 的最小值为……………( )(A)
的最小值为……………( )(A)![]()
(B)![]()
(C)![]()
(D)![]()
10. 要得到函数![]() 的图象,只要把函数
的图象,只要把函数![]() 的图象……( )(A)向右平移
的图象……( )(A)向右平移![]() 个单位(B)向左平移
个单位(B)向左平移![]() 个单位
个单位
(C)向右平移![]() 个单位(D)向左平移
个单位(D)向左平移![]() 个单位
个单位
11.如果![]() ,那么
,那么![]() ……………………………………( )
……………………………………( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12.![]() …………………( )(A)
…………………( )(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二.填空题(每小题4分,共16分)
13.若![]() ,则
,则![]()
14.函数![]() 的单调递增区间为
的单调递增区间为
15.若![]() 则
则![]() 的定义域为
的定义域为
16.若![]() 的定义域为R,周期
的定义域为R,周期![]() ,且
,且
则![]() 的值为
的值为
 答题卷(试卷Ⅱ)
答题卷(试卷Ⅱ)
| 题序 | 1—12 | 13—16 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
| 得分 |
一. ![]() 选择题
选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二. 填空题
13. 14. 15. 16.
三.解答题(本题共48 分)
17.(10分)已知![]()
(1)求实数![]() 的取值范围
的取值范围
(2)当![]() 取最大值时,求
取最大值时,求![]() 的值
的值
(3)并求![]() 的最值
的最值
18.(8分)求![]() 的值
的值
19.(8分)求函数![]() ,
,![]() 的值域
的值域
20.(8分)已知![]() (其中
(其中![]() )
)
求![]()
21. (8分)已知函数![]()
(1)将其化为![]() 的形式其中
的形式其中![]()
(2)指出该函数图象可由![]() 的图象通过怎样的变换而到
的图象通过怎样的变换而到
![]()
 22. (8分)设
22. (8分)设![]() (
(![]() 为常数)求
为常数)求![]() 的值
的值
高一年期中考试试卷参考答案
一、选择题
| A 卷 | 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | D | D | D | A | D | B | A | C | B | B | |
| B 卷 | 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | C | D | C | B | B | B | B | D | D | A |
二、填空题
(A卷) (B卷)
13.![]() 13.
13.![]()
14.![]() 14.
14.![]()
15.![]() 15.
15. ![]()
16.![]() 16.
16. ![]()
三、解答题
17. (A卷)解:
(1)![]()
![]()
∴![]()
(2)当![]() 即
即![]() 时………………
时………………![]()
![]() 取得最大值为
取得最大值为![]() ……………………………………………
……………………………………………![]()
(3)由(1)(2)知
![]()
![]()
又![]()
∴![]() 时,
时,![]()
![]() 时,
时,![]()
18. (A卷)解:

19. (A卷)解:依题意知
![]()
![]()
又![]() ∴
∴![]()
∴当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴该函数的值域为![]()
20.(A卷)解:
![]()
![]()
∴![]()
![]()
又![]() 从而
从而![]()
∴![]()
另解:
∴![]()
![]()
又![]()
∴![]()
∴![]() 从而知
从而知![]()
20.(B卷)解:
![]()
![]()
∴![]()
![]()
又![]() 从而
从而![]()
∴![]()
另解:
∴![]()
![]()
又![]()
∴![]()
∴![]() 从而知
从而知![]()
21. (A卷)解:依题意得
![]()
![]()
![]()
![]()
22. (A卷)解:
(1)![]()
![]()
![]()
![]() (2)
(2)![]() 的图象
的图象
可由![]() 向右平移
向右平移![]() 单位……………………………………
单位……………………………………![]()
再保持纵坐标不变,横坐标缩短到![]() 倍而得到…………………
倍而得到…………………![]()