高一上学期期中测试数学试题
一、选择题(本题共12小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]()
C. ![]() D. f
D. f
2.若集合![]() ,则满足
,则满足![]() 的集合B的个数是 ( )
的集合B的个数是 ( )
A.1 B.2 C.7 D. 8
3.若原命题为“若![]() ,则x, y互为倒数”,则 ( )
,则x, y互为倒数”,则 ( )
A.逆命题真,否命题真,逆否命题真
B. 逆命题假,否命题真,逆否命题真
C.逆命题真,否命题真,逆否命题假
D. 逆命题真,否命题假,逆否命题真
4.若![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.2 B.![]() C.1
D.
C.1
D.![]()
5.已知函数![]() ,那么集合
,那么集合![]()
![]()
中所含元素的个数是 ( )
A.0个 B.1个 C.0个或1个 D.1个或2个
6.不等式![]() 的解集是 ( )
的解集是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.设![]() ┒p是┑q的 ( )
┒p是┑q的 ( )
A.充分不必要条件 B.必要不充分条件
|
8.设函数![]()
![]() ,则函数
,则函数![]() 的图像是 ( )
的图像是 ( )

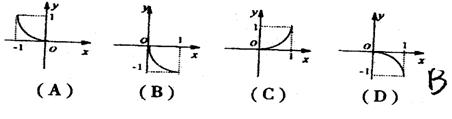
9.若函数![]() 的反函数为
的反函数为![]() ,则
,则![]() 定义域是 ( )
定义域是 ( )
A.[-1, 0] B.[-1, 1] C.[0, 1] D.(-1, 1)
10.不等式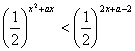 恒成立,则a的取值范围是 ( )
恒成立,则a的取值范围是 ( )
A.[-2, 2] B.(-2, 2) C.[0, 2] D.[-3, 3]
11.已知函数![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 的值 ( )
的值 ( )
A.等于0 B.等于![]() C.等于
C.等于![]() D. 不确定
D. 不确定
12.对一切实数x, y, 函数![]() 满足
满足![]() 且
且![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.1 B.0 C.2 D.–1
二、填空题(本题共4小题,每小题4分,共16分,请把答案填写在答题纸上)
13.已知![]() ,则
,则![]() .
.
14.函数![]() 的单调递减区间是
.
的单调递减区间是
.
15.求函数![]() 的反函数(
的反函数(![]() 且
且![]() )为
.
)为
.
16.老师给出一个函数![]() ,四个学生各指出这个函数的一个性质:
,四个学生各指出这个函数的一个性质:
甲:对于![]() ,都有
,都有![]() ;
;
乙:在![]() 上函数递减;
上函数递减;
丙:在![]() 上函数递增;
上函数递增;
丁:![]() 不是函数的最小值.
不是函数的最小值.
如果其中恰有三人说的正确,请写出这样的一个函数 .
三、解答题(本题共6小题,共56分,请把答案写在答题纸上的指定区域内)
17.(本小题满分8分)已知函数![]()
(1)作出其图像;
(2)由图像指出函数的单调区间;
(3)由图像指出当x取何值时,函数有最值,并求出最值.
18.(本小题满分10分)已知函数![]() 的定义域与函数
的定义域与函数![]()
![]() 的定义域相同,求函数
的定义域相同,求函数![]() 的值域.
的值域.
19.(本小题满分12分)已知函数![]()
![]()
(1)求![]() 的定义域,值域;
的定义域,值域;
(2)讨论并证明![]() 在
在![]() 上的单调性.
上的单调性.
20.(本小题满分12分)国家收购某种农产品价格为每吨120元,共中征税标准为每100元征收8元(称税率为8个百分点),计划可以收购a万吨,为减轻农民负担,决定税率降低x个百分点,预计收购量可增加2x个百分点。如下表:
| 原计划 | 调整税率后 | |
| 收购量 | a万吨 |
|
| 每吨价 | 120元 | |
| 征税标准 | 8% |
|
(1)写出降低税率后税收y(万元)与x的函数关系式:
(2)要使此项税收在税率调整后不低于原计划的78%,试确定x的范围.
21.(本小题满分14分)已知全集![]() ,
,![]() ,求实数a的取值范围,分别使:
,求实数a的取值范围,分别使:
(1)![]()
(2)![]() .
.
数学试题参考答案及评分标准
一、选择题:
1. B 2. D 3. A 4. C 5. C 6. D 7. A 8. B 9.C 10. B 11. A 12. A
二、填空题:
13. x
14. ![]() 15.
15. ![]()
16. ![]() (答案不唯一)
(答案不唯一)
三、解答题:
17.解:(1) 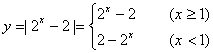 ………………………………………4¢
………………………………………4¢
(2)单调减区间:![]() 单调增区间:
单调增区间:![]() ………………………………6¢
………………………………6¢
(3)当x![]() 时,函数有最小值,
时,函数有最小值,![]() ………………………………………8¢
………………………………………8¢
18.解:![]() …………………………………………………………2¢
…………………………………………………………2¢
设![]() 则
则![]() …………4¢
…………4¢ ![]() ……………6¢
……………6¢
当 ![]() ;当
;当![]() ……………………………………8¢
……………………………………8¢
∴ ![]() ……………………………………………………10¢
……………………………………………………10¢
19.解:(1)![]() ∴
∴![]() 定义域
定义域![]() }……………………………2¢
}……………………………2¢
![]() ∴
∴![]() ……………………4¢
……………………4¢
(2)设![]() 又
又![]() ,则
,则![]()
![]() …………………………8¢
…………………………8¢
当![]() 时
时![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上递减;……………………………………………………10¢
上递减;……………………………………………………10¢
当![]() 时
时![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上递增;…………………………………………………12¢
上递增;…………………………………………………12¢
20.解:(1)![]() ,其中
,其中![]() ……………………………6¢
……………………………6¢
(2)由条件![]()
解得:![]() 。…………………………………………12¢ 答略
。…………………………………………12¢ 答略
21.解:∵ ![]() ,
,
![]() 。
。
∴ ![]() ………………2¢ 当
………………2¢ 当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() 。………………………5¢
。………………………5¢
(1)当![]() ,则
,则
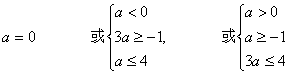
∴ ![]() ……………………………………………10¢
……………………………………………10¢
(2)![]() 若
若![]() ,则
,则
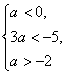 ∴
∴ ![]() 。…………………………………14¢
。…………………………………14¢