高一(上)学期数学练习 (命题人:刘锦)
一、选择题:
1、 设u={0,1,2,3,4},A={0,1,2,3},B={2,3,4},则(CuA)![]() 的值为( )
的值为( )
(A){0} (B){0,1} (C){0,1,2,3,4} (D){0,1,4}
2、 如是(x,y)在映射f下的象是(x+y,x-y),那么(4,2)在f下的原象是( )
(A)(-3,1) (B)(3,-1) (C)(3,1) (D)(-3,-1)
3、 已知:p:3+3=5,q:5>3,则下列判断中错误的是 ( )
(A)p或q为真,非q为假 (B)p或q为真,非p为真
(C)p且q为假,非p为假 (D)p且q为假,p或q为真
4、“p或q为真命题”是:“p且q”为真命题的 ( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要
5、已知![]() 为
( )
为
( )
(A) 1 (B)9 (C)3 (D)8
6、若不等式![]() 的解集为(-
的解集为(-![]() ,),则
,),则![]() 的值为( )
的值为( )
(A)10 (B)-10 (C)14 (D)-14
7、函数![]() 的反函数是
( )
的反函数是
( )
(A)y=![]() (B)y=
(B)y=![]()
(C)y=![]() (D)
(D)![]()
8、设![]()
![]() ,则
,则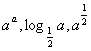 之间的大小关系为
( )
之间的大小关系为
( )
(A)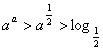
![]() (B)
(B)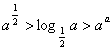
(C)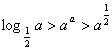 (D)
(D)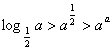
9、设函数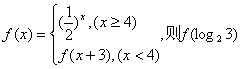 的值为 ( )
的值为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10、函数![]() 在
在![]() 时有最大值
时有最大值![]() 的范围为( )
的范围为( )
(A)![]() (B) a>2 (C)
(B) a>2 (C)![]() (D)a<0
(D)a<0
11、在等差数列{![]() }中3
}中3![]() ,则数列前13项之和为
( )
,则数列前13项之和为
( )
(A)156 (B)52 (C)26 (D)13
12、数列{![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,则
的等比数列,则![]() 等于
( )
等于
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
13、已知等比数列![]() 的公比
的公比![]() 等于( )
等于( )
(A)![]() (B)-3
(C)
(B)-3
(C)![]() (D)3
(D)3
14、![]() 是公差为-2的等比数列,如果
是公差为-2的等比数列,如果![]() ,那么
,那么![]() 的值是 ( )
的值是 ( )
(A)-82 (B)-78 (C)-148 (D)-182
15、数列![]() 的前n项和为 ( )
的前n项和为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题:
16、设A=![]() ,B=
,B=![]() 全集U=R,那么(CuA)
全集U=R,那么(CuA)![]()
17、函数![]() 的单调递增区间是
。
的单调递增区间是
。
18、函数y=![]()
![]() 的定义域为
的定义域为
19、函数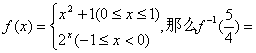
20、若不等式![]() 对一切实数x恒成立,则实数a的取值范围是
。
对一切实数x恒成立,则实数a的取值范围是
。
21、函数![]() 的值域为
。
22、已知数列{
的值域为
。
22、已知数列{![]() }的前n项和
}的前n项和![]() 则
则![]()
23、数列![]() 中,
中,![]() ,那么
,那么![]() 的值是
。
的值是
。
24、已知等比数列![]() 中,
中,![]() ,则由此数列的偶数项所组成的新数列前n项和Sn的值为
。
,则由此数列的偶数项所组成的新数列前n项和Sn的值为
。
25、数列![]() 的通项公式是
的通项公式是![]() ,若前n项和为10,则项数n=
,若前n项和为10,则项数n=
三、解答题: 26、已知![]()
![]() 且
且![]() 是一个
是一个
递增的等差数列![]() 的前三项,求(1)
的前三项,求(1)![]() 的通项公式。(2)求
的通项公式。(2)求![]() 的值。
的值。
27、已知函数![]()
(1) 判断函数f(x)在(-1,1)的单调性。
(2) 求函数f(x)的值域。
28、一个数列![]() 中,当n为奇数时,
中,当n为奇数时,![]() ,当n为偶数时,
,当n为偶数时,![]() ,求数列的前2n项之和。
,求数列的前2n项之和。
29、为成功举办北京2008年奥运会,针对北京地区已发生的多起沙尘暴,北京市早在1994年底年就对某郊县的沙漠地区进行治理,从1995年起在沙漠上植树,改造沙漠为森林,以后每年都比上一年多种植相同面积的树木改造沙漠,据统计,沙漠总面积以及每年的植树面积如图所示,问按此计划预计哪一年可将沙漠改造完毕?
![]()
![]()
![]() 面积(亩)
面积(亩)
![]() 面积(亩)
面积(亩)
![]()
![]()
![]()
![]() 25200
1400
25200
1400
![]()
![]()
![]()
![]() 24000
1000
24000
1000
![]()
![]() 0
95 96 年份
x 0 95
96 年份x
0
95 96 年份
x 0 95
96 年份x
沙漠总面积 每年植树面积
高一(上)学期数学练习题答案 (供稿人:刘锦)
一、选择题:
D C C B B D A C D C C A B A B
二、填空题:
16、{-2}
17、![]() 18、[3,4
18、[3,4![]() 19、
19、![]() 20、[0,
20、[0,![]()
21、![]() 22、-85 23、5(q-p) 24、
22、-85 23、5(q-p) 24、![]() 25、120
25、120
三、解答题:
26、解:由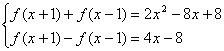 得
得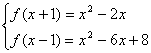
由![]() ,由
,由![]() 是递增的等差数列,得
是递增的等差数列,得![]()
![]() , 当x=2时,
, 当x=2时,
![]()
![]()
即x=3时,![]()
(1)![]() 是递增的等差数列
是递增的等差数列![]() 的前三项,
的前三项,![]()
![]()
(2)![]() 首项为
首项为![]() 的等差数列的前9项和。
的等差数列的前9项和。![]() =
=![]()
=![]()
27、解:(1)令![]() , 则有
, 则有![]() =
=![]() =
=![]()
=![]() =
=![]()
![]()
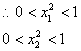 且
且![]() 于是
于是
![]() 即
即![]() (-1,1)内是递增函数。
(-1,1)内是递增函数。
(2)当![]()
①当![]()
②当![]() 。
。
28、![]()
∴奇、偶数项对半开各有m项。
当n为奇数时, 当n为偶数时,
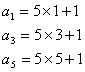
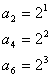
![]()
![]()
![]()
![]()
∴S![]()
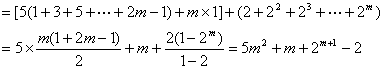
29、解:设该县1994年底有沙漠m亩,以后每年被沙漠化的土地面积为y亩,从1995年起,每年植树面积成等差数列![]() ,
,
d=1400-1000=400,到第n年年底植树总面积为Sn,则![]() ,
,![]() ,到第n年年底沙漠的总面积为
,到第n年年底沙漠的总面积为![]()
![]()
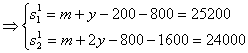
![]()
∴S![]() 时,得
时,得
![]()
∴![]()
答:到2004年年底可将沙漠改造完毕。