高一第二学期数学期末复习试卷（六）
时量：100分钟 满分：120分 班级： 姓名：
一、选择题：本大题共10小题，每小题3分，共30分.
1.
已知
是
的
边上的中线，若
、
，则
等于 。
A.
B.
C.
D.
2.
点
分
所成的比为
，则下列结论正确的是
。
A.点分
的比为 B.点
分
的比为
C.点
分
的比为
D.点分的比为
3.
按向量将点
平移到点
，则按向量将点
平移到 。
A.
B.
C.
D.
4.
函数
与函数
的周期之和为
，则正实数
的值为 。
A.
B. C.
D.
5.
已知
，则
等于 。
A.
B.
C.
D.
6.
已知平行四边形
满足条件
，则该四边形是 。
A.矩形 B.菱形
C.正方形 D.任意平行四边形
7.
已知向量
，若
，则的值是 。
A.
B.
C.
D.
8.
与向量
垂直的单位向量坐标为
。
A.
或
B.
或
C.
或
D.
或
9.
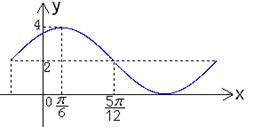
已知函数
的一部分图象如右图所示，如果
，则 。
A.
B.
C.
D.
10.
角
满足条件
，则在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题：本大题共6小题，每小题3分，共18分.
11.
已知
，
，则
的值为__________________________；
12.
函数
的定义域是_____________________________________________；
13.
已知向量与的夹角为
，且
，则在方向上的投影是________；
14.
在教学楼的楼顶看奥林匹克大楼楼顶的仰角为
，看楼底的俯角为
，已知教学楼的高为
米，则奥林匹克大楼高为______________米（精确到米，计算时可参考以下数据：
）；
15.
方程
有解，则实数
的取值范围是___________________________；
16.
给出下列命题：
①函数
是偶函数；
②函数
在闭区间
上是增函数；
③直线
是函数
图象的一条对称轴；
④将函数
的图象向左平移
单位，得到函数
的图象；
其中正确的命题的序号是： ；
三、解答题：本大题共5小题，共52分，解答应写出文字说明、证明过程或演算步骤.
17.
（8分）求函数
的最大、最小值，并求取得此最值时相应的的取值集合；
18.
（12分）已知、
、
分别是的三个内角、、所对的边
【Ⅰ】若面积
求、的值；
【Ⅱ】若
，且
，试判断的形状．
19.
（12分）已知三个顶点的坐标分别为
、
、
【Ⅰ】若
是边上的高，求向量
的坐标；
【Ⅱ】若点
在
边上，且
，求点的坐标；
20.
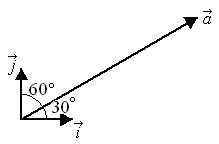（10分）如图
，在同一平面内，向量与单位向量
、
的夹角分别为
、
，已知
.
【Ⅰ】以和为基底，表示；
【Ⅱ】若
，求与的夹角
的值；
21.
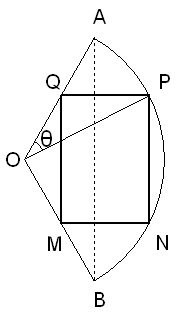
（10分）某校在申办国家级示范校期间，征得一块形状为扇形的土地用于建设田径场，如下图所示，已知扇形角
，半径
米，按要求准备在该地截出内接矩形
，并保证矩形的一边平行于扇形弦
，设
，记
.
【Ⅰ】以为自变量，写出
关于的函数关系式；
【Ⅱ】当为何值时，矩形田径场的面积最大，并求最大面积；
