高一年级数学教学质量检测试题卷
考生须知:
1. 本卷满分100分, 考试时间90分钟.
2. 答题前, 在答题卷密封区内填写学校、班级和姓名.
3. 所有答案必须写在答题卷上, 写在试题卷上无效.
4. 考试结束, 只需上交答题卷.
一.选择题 : 本大题共12小题, 每小题3分, 共36分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的 .
1. 数列{a n}中, 若a 1=3, a n+1= a n – 2 (nÎN ), 则a n= ( )
(A) 1 – 2n. (B) 2n + 1. (C) 5 –2n.. (D) 2n + 5.
2. 下列向量中,可以不共线的一组向量是( )
(A) a= –2e , b = 2e. (B) a= e1 –e2, b = –2 e1 +2e2.
(C) a= 4e1 –![]() e2, b = e1 –
e2, b = e1 –![]() e2. (D) a = e1 + e2, b = 2 e1 – 2e2.
e2. (D) a = e1 + e2, b = 2 e1 – 2e2.
3.函数y = 10x –1的反函数是 ( )
(A) y = lgx + 1( x > –1 ) . (B) y = lg(x-1)( x > 1 ).
(C)y = lgx – 1 ( x >0) . (D) y = lg(x + 1)( x >–1) .
4. 将函数y = log22x的图象F按向量a = (2,–1)平移到F¢,则F¢的解析式为( )
(A) y = log2(2x – 4) – 1 . (B) y = log2(2x + 4) – 1 .
(C) y = log2(2x + 4 ) +1 . (D) y = log2(2x – 4 ) + 1 .
5. 函数y = Asin (wx + j)在同一周期内,当x =![]() 时, y取最大值2 ; 当x =
时, y取最大值2 ; 当x = ![]() 时, y取最小值–2 , 则该函数的解析式是 (
)
时, y取最小值–2 , 则该函数的解析式是 (
)
(A) y = 2sin (x +![]() ).
(B) y = 2sin (2x +
).
(B) y = 2sin (2x +![]() ).
).
(C) y = 2sin (![]() –
–![]() ).
(D) y = 2sin (2x +
).
(D) y = 2sin (2x +![]() ).
).
6. 已知集合A = { x ![]() £ 0 }, B = { x 2x + 1 > 5 }, S = R,
则ÚS(A∩B)等于 ( )
£ 0 }, B = { x 2x + 1 > 5 }, S = R,
则ÚS(A∩B)等于 ( )
(A) { x x £ 2或x > 3}. (B) { x 2 < x £ 3 }.
(C) { x x < 2或x ³ 3 }. (D) { x –2 £ x £ 3}.
7. 已知a+ b =![]() , 则cosacosb –
, 则cosacosb –![]() sinacosb –
sinacosb –![]() cosasinb – sinasinb 的值为 ( )
cosasinb – sinasinb 的值为 ( )
(A) –![]() . (B) –
. (B) –![]() (C)
(C) ![]() . (D)
. (D) ![]() .
.
8. 据调查发现,某湿地的面积在最近50年内减少了10%. 如果按此规律,设2000年该湿地的面积为m km2,则经过x年,湿地的面积y与x的函数关系是 ( )
(A)![]() .
(B)
.
(B)![]()
(C)![]() .
(D)
.
(D)![]() .
.
|
(第9题) |
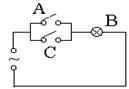
9. 如图电路中,规定“开关A的闭合”为条件M,“灯泡B亮”为结论N,观察以下图1和图2,可得出的正确结论分别是 ( )
(A)M是N的充分而不必要条件.
(B)M是N的必要而不充分条件.
(C)M是N的充要条件.
(D)M是N的既不充分也必要不条件.
10. 甲船在千岛湖B岛的正南A处,AB = 3km. 甲船以8 km / h的速度向正北方向航行,同时乙船自B岛出发以12 km/ h的速度向北偏东60°的方向驶去,则行驶15分钟,两船之间的距离是( )
(A) ![]() km. (B)
km. (B) ![]() km. (C)
km. (C)![]() km. (D)
km. (D)![]() km.
km.
11. 已知A为三角形的一个内角,函数y = x2cosA – 4xsinA + 6 , 对于任意实数x都有y > 0,则角A的取值范围是 ( ).
(A)0<A<![]() . (B)
. (B)![]() <A≤
<A≤![]() . (C)
. (C)![]() <A<p. (D)0 < A< p .
<A<p. (D)0 < A< p .
12.一个递增的整数数列a1, a2 , a3, … 满足条件:a n + 2 = a n+1 + a n (n ÎN*), 若a5 = 59, 则首项a1的最大值是 ( )
(A) 4. (B) 7. (C) 10. (D) 11.
二.填空题:本大题有5小题, 每小题4分, 共20分. 请将答案填写在答题卷中的横线上.
13.log318 – log32 = .
14. 在△ABC中, 若A = 60°, B = 75°, c = 6 , 则a = .
15. 在直角坐标系中,![]() = (
= (![]() ,
,![]() ) ,
) , ![]() = 2, 且
= 2, 且![]() ·
·![]() = 0, 则点B的坐标是 .
= 0, 则点B的坐标是 .
|
(第17题) |
16. 若cos2a = ![]() , 则sin4a – cos4a = .
, 则sin4a – cos4a = .
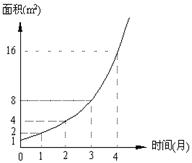
17.某池塘中野生水葫芦的面积与时间的函数关系的图象,如右图所示. 假设其关系为指数函数,并给出下列说法:
(1) 此指数函数的底数为2;
(2) 在第5个月时,野生水葫芦的面积就会超过30m2;
(3) 野生水葫芦从4m2蔓延到12m2只需1.5个月;
(4) 设野生水葫芦蔓延到2m2,3m2, 6m2所需的时间分别为t1, t2, t3, 则有t1 + t2 = t3;
(5) 野生水葫芦在第1到第3个月之间蔓延的平均速度等于在第2到第4个月之间蔓延的平均速度;
其中正确的说法有 . (请把正确说法的序号都填在横线上)
三.解答题:本大题有4小题, 共44分. 解答应写出文字说明, 证明过程或演算步骤.
18.(本小题满分10分)
设函数f ( x ) = ![]() (sinx – cosx)2 x ÎR .
(sinx – cosx)2 x ÎR .
(1) 求函数f ( x )的最小正周期T;
(2) 当x为何值时,函数f ( x )取最大值?并求出这个最大值.
19. (本小题满分8分)
设i , j 是平面直角坐标系内x轴,y轴正方向上的两个单位向量,且![]() = 4i + 2j ,
= 4i + 2j ,![]() = 3i + 4 j . 试证:△ABC是直角三角形.
= 3i + 4 j . 试证:△ABC是直角三角形.
20. (本小题满分12分)
(1) 画出函数g (x ) = x2 – 2x 的图象;
(2) 证明函数f ( x ) = x + ![]() 在(0,1]上单调递减.
在(0,1]上单调递减.
21 (本小题满分14分)
某次国际网球邀请赛共有128位选手参加,比赛采用单淘汰制,即每轮淘汰一半的选手,剩下一半的选手进入下一轮. 在第1轮被淘汰的每位选手可获得出场费1万元,在第2轮被淘汰的选手可获得2万元,在第k轮被淘汰的选手可获得2 k – 1 万元,而冠军则可获得128万元.
(1)求本次网球邀请赛共需出场费多少万元?
(2)设网球场有3000个坐位,第一轮比赛门票价格为a元( a为整数),第二轮比赛门票价格为a + 50元,第k轮比赛门票价格为a + 50(k – 1 )元. 假设每场比赛均满座,且每张门票可观看一轮的所有比赛,则要使本次邀请赛不亏本,第一轮门票价格a应该如何确定?
高一年级教学质量检测
数学参考答案
一.选择题 : 本大题共12小题, 每小题3分, 共36分..
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | D | D | A | B | A | B | A | A | B | A | C |
二.填空题:本大题有5小题, 每小题4分, 共20分.
13.2 . 14. 3![]()
15.(0,2![]() ),(2
),(2![]() ,0)
. 16. –
,0)
. 16. –![]()
17(1)(2)(4) .
三.解答题:本大题有4小题, 共44分.
18.(本小题满分10分)
解 (1) f ( x ) = ![]() (1 – 2sinxcosx) =
(1 – 2sinxcosx) = ![]() –
–![]() sin2x.
4分
sin2x.
4分
∴ T = p. 2分
(2) x = kp –![]() (
k ÎZ )时,
f ( x )max = 2
(
k ÎZ )时,
f ( x )max = 2![]() .
4分
.
4分
19. (本小题满分8分)
证1:∵i , j 是平面直角坐标系内x轴,y轴正方向上的两个单位向量,
∴ i =1, j = 1, 且i⊥j , 即i • j =0.
∵![]() =
=![]() –
–![]() =–i + 2 j ,
4分
=–i + 2 j ,
4分
∴![]() ·
·![]() = – 4 + 4 = 0,
= – 4 + 4 = 0,
∴∠B = 90°,即△ABC是直角三角形. 4分
证2. ∵i , j 是平面直角坐标系内x轴,y轴正方向上的两个单位向量,
∴ i =1, j = 1, 且i⊥j , 即i • j =0.
又∵![]() = 4i + 2j ,
= 4i + 2j ,![]() = 3i + 4 j ,∴
= 3i + 4 j ,∴![]() =
=![]() ,|
,|![]() |=5,cos<
|=5,cos<![]() ,
,![]() >=
>=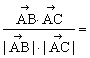
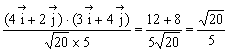 . 4分
. 4分
从而![]() = 5 .
= 5 .
∴|![]() |2+|
|2+|![]() |2=|
|2=|![]() |2,故△ABC是直角三角形.
4分
|2,故△ABC是直角三角形.
4分
20. (本小题满分12分)
解 (1)法1:
g ( x ) =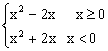 ,
3分
,
3分
画图象正确 3分
法2
证明f ( x )为偶函数, 2分
画x ³ 0时,f ( x ) = x2 – 2x 图象, 2分
将画出图象关于y轴对称. 2分
(2) 设0 < x1 < x2 £ 1, 则f ( x1)
– f ( x 2) = ![]() +x1 –
+x1 –![]() –x2 =
–x2 = ![]() + ( x1 – x 2)
+ ( x1 – x 2)
= ( x1 – x2)
( 1 – ![]() ) = (x1 – x2)
) = (x1 – x2) ![]() . 3分
. 3分
∵x1 < x2 , ∴x1 – x2 <0 ;
又∵0 < x1 <1 , 0< x2 £ 1 . ∴ 0< x1 x2 < 1 , ∴x1x2 –1 < 0 .
∴f ( x1) – f ( x 2) > 0 , 即f ( x1) > f ( x 2);
所以当0 < x £ 1时,函数单调递减. 3分
21 (本小题满分14分)
解(1)设奖金总数为W万元.则有
W = 64´1 + 32´2 + 16´22 + 8´23 + 4´24 + 2´25 + 1´26 + 27
= 7´26 + 27 = 9´26 (万元). 5分
(2) 设门票收入为y元,则
y = 3000[a + ( a + 50 ) + ( a + 100 ) + (a +150) + ( a + 200 ) + ( a +250) + ( a +300 ) ]
= 3000( 7a +1050 ) . 5分
比赛不亏本,则3000[7a + 1050] ³ 90000´26 .
解得 a ³ 124.3
答:要使邀请赛不亏本,第一轮价格至少要定为125元. 4分