学习攻关
基础测试
（一）选择题（每题3分，共30分）
1．在下列各角中，第三象限角是（ ）．
（A）－540° （B）－150°
（C）－225° （D）510°
【提示】第三象限角a 满足180°＋k ·360°＜a ＜270°＋k·360°，k∈Z．
【答案】（B）．
【点评】
本题考查终边相同的角的概念．与－540°终边相同的角为180°，为轴线角，故排除（A）；与－225°终边相同的角为135°，为第二象限角，故排除（C）；与510°终边相同的角为150°，也是第二象限角，排除（D）．
2．若a 是第四象限角，则p －a 是 （ ）．
（A）第一象限角 （B）第二象限角
（C）第三象限角 （D）第四象限角
【提示】由a 是第四象限角，得－a 为第一象限角，p＋（－a）为第三象限角．
【答案】（C）．
【点评】本题考查象限角之间的关系．
3．Sin 600°的值是（ ）．
（A）
（B）
（C）
（D）
【提示】sin 600°＝sin 240°＝－sin 60°＝－．
【答案】（D）．
【点评】本题是1998年高考题，主要考查诱导公式及特殊角的三角函数值．利用诱导公式可以把求任意角的三角函数值的问题转化为求某锐角的三角函数值．
4．若b＞a＞0，且tan a ＝
，sin a ＝
，则a 的集合是（ ）．
（A）｛a 0＜a ＜
｝
（B）｛a 
＋2k p
ap＋2k p，k∈Z｝
（C）｛a 2k pap＋2k p，k∈Z｝
（D）｛a 
＋2k p＜a＜p＋2k p，k∈Z
【提示】由已知，tan a ＜0，sin a ＞0 ，且a
b，即
0，故a 是第二象限角．
【答案】（D）．
【点评】本题考查由三角函数值的符号确定角所在的象限．
5．函数y＝tan（x＋
）的定义域是（ ）．
（A）{x∈R x
k p＋
，k∈Z }
（B）{ x∈R xkp－，k∈Z }
（C）{ x∈R x2kp＋，k∈Z }
（D）{ x∈R x2kp－，k∈Z }
【答案】（A）．
【点评】本题考查正切函数定义域．
6．在下列函数中，以为周期的函数是（ ）．
（A）y＝sin 2x＋cos 4x
（B）y＝sin 2x cos 4x
（C）y＝sin 2x＋cos 2x
（D）y＝sin 2x cos 2x
【提示】可以根据周期函数的定义对四个选项逐个进行验证．
【答案】（D）．
【点评】本小题考查三角函数的周期性．
由于sin 2（x＋）＋cos 4（x＋）
＝sin（2x＋p）＋cos（4x＋2p）
＝－sin 2x＋cos 4xsin 2x＋cos 4x，排除（A）；
由于sin 2（x＋）cos 4（x＋）
＝－sin 2x cos 4xsin 2x cos 4x，排除（B）；
由于sin 2（x＋）＋cos 2（x＋）
＝－sin 2x－cos 2xsin 2x＋cos 2x，排除（C）；
而sin 2（x＋）cos 2（x＋）
＝sin 2x cos 2x，故选（D）．
实际上y ＝sin 2x cos 2x＝ sin 4x，其周期为．
7．已知q 是第三象限角，且sin 4 q＋cos 4 q ＝
，那么sin 2q 等于( )．
（A）
（B）－
（C）
（D）－
【提示】
sin4 q＋cos4 q ＝（sin2 q ＋cos2 q）2－2 sin2 q cos2 q ＝1－ sin2 2q ，得sin2 2q ＝
，再由q
是第 三象限角，判断sin 2q 大于0．
【答案】（A）．
【点评】本题考查同角三角函数公式、二倍角公式及三角恒等变形的能力．
8．函数y＝－3 cos（－2 x＋
）的图象可由y＝－3 cos（－2x）的图象（ ）．
（A）向左平行移动个单位长度得到
（B）向右平行移动个单位长度得到
（C）向左平行移动
个单位长度得到
（D）向右平行移动个单位长度得到
【提示】y＝－3 cos[－2（x－）] ＝－3 cos（－2x＋）．
【答案】（D）．
【点评】本题考查三角函数的图象和性质．
9．
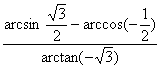的值等于（ ）．
（A）2 （B）－2 （C）1 （D）－1
【提示】arcsin＝，arcos()＝
，arctan（－
）＝－．
【答案】(C)．
【点评】本题考查反正弦.、反余弦、反正切的定义及特殊角的三角函数值．
10．若q 三角形的一个内角，且函数y＝x2 cos q －4x sin q ＋6对于任意实数x均取正值，那么cos q 所在区间是（ ）．
（A）（，1）
（B）（0，） （C）（－2，） （D）（－1，）
【提示】
对于任意实数x，函数y均取正值必满足a＞b，且判别式
＜0＜p，有－1＜cos
q ＜1．由不等式组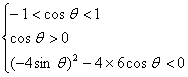 
解得 ＜cos q ＜1．
【答案】（A）．
【点评】本题结合二次函数的性质考查三角函数的有关知识．
（二）填空题（每题4分，共20分）
1．终边在坐标轴上的角的集合是_________．
【答案】{a a ＝
，k∈Z }
【点评】本题考查轴线角的概念．
2．求
的值等于___________．
【提示】
＝cos（＋
）＝－sin ．
【答案】－
．
【点评】本题考查诱导公式，二倍角公式以及特殊角的三角函数值．
3．tan 20°＋tan 40°＋ tan 20°tan 40°的值是___________．
【提示】利用公式tan(a＋b ) ＝
的变形
tan a＋tan b＝tan(a＋b )（1－tan a tan b），得
tan 20°＋tan 40°＋（tan 20°tan 40°）
＝tan（20°＋40°）（1－tan 20°tan 40°）＋ tan 20°tan 40°＝．
【答案】．
【点评】本题通过两角和的正切公式的逆向使用考查三角恒等式的变形及计算推理能力．
4．若sin（＋a）＝
，则cos 2a ＝__________．
【提示】依题意，cos a ＝，则cos 2 a＝2 cos2 a
－1＝－
．
【答案】－．
【点评】本题考查诱导公式与二倍角余弦公式．
5．函数y＝2 sin x cos x－2 sin2 x＋1的最小正周期T ＝__________．
【提示】y＝sin 2x＋cos 2 x ＝
sin（2 x＋
）．
【答案】p．
【点评】本题考查二倍角正弦余弦，两角和的三角函数及三角函数y＝Asin（w x＋j）的周期性．
（三）解答题（每题10分，共50分）
1．化简（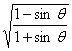
－
）（
－
）．
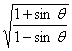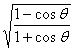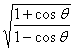【提示】解求题的关键是设法去掉根号，将无理式化为有理式，如
＝
＝
＝
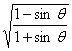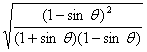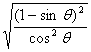．其它三个根式类似．
【答案】
原式＝（－
）（
－
）＝
．
由题设，sin q cos q
0，
当sin q 与cos q 同号，即kp＜q＜kp＋（k∈Z）时，原式＝4；
当sin q 与cos q 异号，即kp＜q＜kp＋（k∈Z）时，原式＝－4．
【点评】本题考查三角函数值的符号、同角三角函数公式以及三角函数的恒等变形的能力．本题也可将结果进一步化为
直接讨论sin 2q 符号．
2．设a 是第二象限角，sin a ＝，求sin (
－2a)的值．
【提示】因为sin (－2a )＝sin (6p＋－2a )＝sin (－2a)，只要利用已知条件，算出sin 2a，cos 2a 就可以了．
【答案】∵ a 是第二象限角，sin a ＝，
∴ cos a ＝－
，
∴ sin 2a ＝2 sin a cos a
＝－
，
cos 2a ＝1－2 sin2 a ＝．
sin (
－2a )＝sin (－2a )＝ sin cos 2a
－cos sin 2a ＝
．
【点评】本题考查诱导公式，同角三角函数关系式，二倍角公式，两角和与差的正弦余弦，及计算能力．
3．已知
＝k（
＜a
＜
，试用k表示sin a －cos a 的值．
【提示】
先化简＝2 sin a
cos a
，再利用（sin a －cos a）2＝1－2 sin a cos a 即可．
【答案】
∵
＝
＝
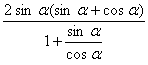
＝2 sin a cos a
＝sin 2a ＝k ≤1．
而（sin a－cos a）2＝1－sin 2a ＝1－k，
又＜a
＜，于是sin a
－cos a ＞0，
∴ sin a －cos a ＝
．
【点评】
本题考查二倍角公式，同角三角函数关系及运算能力．
5．求证
＝1＋tan 2
a ＋sin 2
a．
【提示一】通过将右边的式子作“切化弦”的变换．
【提示二】通过化“1”进行变换，可以将sin2 a ＋cos2 a 化成1，也可以根据需要将1化成sin2 a＋cos2 a ．
【答案一】右边＝1＋
＋sin2 a
＝
＝
＝
＝
＝
＝左边
【答案二】
左边＝
＝
＝
＝
＝
＝＋1＋sin2 a
＝1＋tan 2 a＋sin 2 a
＝右边．
【点评】
本题考查三角恒等式的证明．【答案一】和【答案二】均采用了综合法，即从已知条件出发，将左边（或右边）进行恒等交换，逐步化成右边（或左边）．本题也可以采用分析法，即从求证的等式出发，递推到已知．
5．若函数f（x）＝a＋b cos x＋c sin x的图象过（0，1）与（，1）两点，且x∈[0，]时， f（x）2，求a的取值范围．
【提示】
根据函数f（x）的图象经过两个已知点，可得到b、c关于a的表达式，代入f（x）的解析式中，得f（x）＝a＋（1－a）sin (x＋)，再利用 f（x）2，可得a的取值范围．
【答案】
∵ 函数f（x）的图象经过点（0，1）及（，1），
∴ 
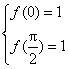即
．
从而b＝c＝1－a．
∴ f（x）＝a＋（1－a）cos x＋（1－a）sin x＝a＋（1－a）sin(x＋)．
由于x∈[0，]，得x＋∈[，
]，
∴ sin(x＋)∈[
，1]．
①当a1时，1－a
0，f（x）∈[1，a＋（1－a）]，而 f（x）2，有1f（x）2．
∴ a＋（1－a）2，
即a∈[－，1]．
②当a＞１时，1－a＜0，f （x）∈[a＋（1－a），1]，
因f （x）2，得－2f （x）1．
∴ －2 a＋（1－a），
即a∈
．
综上，－a４＋
即为所求．
【点评】
本题考查两角和的正弦公式，三角函数的值域以及综合运用函数、不等式等有关知识解决问题的能力．