提高测试（二）
（一）选择题（每题3分，共30分）
1．“a＝1”是“函数y＝cos2 ax－sin2 ax的最小正周期为 p ”的（ ）．
（A）充分而不必要条件
（B）必要而不充分条件
（C）充要条件
（D）既不充分也不必要条件
【提示】
由于y＝cos2 ax－sin2 ax＝cos 2ax，当a＝1时，函数的最小正周期为p ，当a＝－1时，函数的最小正周期也是p ，所以 a＝1是函数的最小正周期为p 的充分而不必要条件．
【答案】（A）．
【点评】本题考查倍角公式和三角函数的周期性以及充要条件的知识．
2．函数f（x）＝M sin（wx＋j）（w ＞0）在区间[a，b]上是增函数，且f（a）＝－M，
f（b）＝M，则函数g（x）＝M cos（w x＋j）在[a，b]上（ ）．
（A）是增函数
（B）是减函数
（C）可以取得最大值M
（D）可以取得最小值－M
【提示】
利用特殊值法，令M＝w ＝1，j
＝0，则有 f（x）＝sin x，g（x）＝cos x，同时a＝－
，b＝，可见，g（x）在[a，b]（即[－，]）上既不是增函数，也不是减函数，但可以取得最大值1，故排除（A）、（B）、（D）．本题也可以用作图法求解．
【答案】（C）．
【点评】本题考查正弦函数、余弦函数的性质以及灵活运用这些知识解决问题的能力．
3．已知a 、b 是锐角三角形的两个内角，则下列各式中成立的是（ ）．
（A）cos a ＞sin b ，cos b ＞sin a
（B）cos a ＜sin b ，cos b ＜sin a
（C）cos a ＞sin b ，cos b ＜ sin a
（D）cos a ＜sin b ，cos b ＞sin a
【提示】
a 、b 是锐角三角形的两个内角，所以a ＋b ＞90°，a ＞90°－b ，故有
sin a ＞sin（90°－b），cos a ＜cos（90°－b），即sin a ＞cos b ，cos a ＜sin b．
【答案】（B）．
【点评】本题考查诱导公式以及正弦函数、余弦函数的单调性．
4．下列不等式中正确的是（ ）．
（A）e cos 52°＜e cos 53°
（B）
＞
（C）
＞
（D）
＜
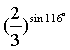
【提示】利用函数的单调性．
【答案】（A）．
【点评】
本题综合指数函数、对数函数的性质考查三角函数的单调性．由于cos 52°＞cos 53°，得ecos 52°＞ecos 53°，排除（A）；由于tan 200°＝tan 20°，tan 199°＝tan 19°，有
tan 20°＞tan 19°，而0＜
＜1，得
＜
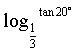，排除（B）；由于
＜
，p ＞1，得
＜
，排除（C）；而sin 115°＞sin 116°，且0＜
＜1，有
＜
．故选（D）．
5．设k是4的倍数加上1的自然数，若以cos x表示cos k x时，有cos k x＝f（cos x），则sin k x等于（ ）．
（A）f（cos x） （B）f（sin x） （C）f（cos k x） （D）f（sin k x）
【提示】
由于sin a ＝cos（
－a），设k＝4n＋1，（n＝0，1，2，…），则有
f（sin x）＝f（cos（－a））＝
＝
＝cos[2np＋－（4n＋1）x]
＝cos[－（4n＋1）x]
＝sin[（4n＋1）x]
＝sin k x ．
以上各步均可逆．
【提示二】
利用特殊值法，令k＝5，则f（cos x）＝cos 5x
sin 5x．排除（A），f（cos 5x）＝
cos（5×5x）＝cos 25xsin 5x，排除（C），f（sin 5x）＝f [cos（－5x）]＝
＝cos（－25x）＝sin 25xsin 5x，排除（D），而f（sin x）＝f [cos（－x）]＝
＝cos（－5x）＝sin 5x．
【答案】（B）．
【点评】本题考查函数的概念，诱导公式以及分析问题、解决问题的能力．
6．已知f（x）＝
，则当q
（
，
）时，式子f（sin 2q ）的值是（ ）．
（A）2 sin q （B）2 cos q （C）－2 sin q （D）－2 cos q
【提示】
f（sin 2q ）－f（－sin 2q ）
＝
－
＝
－
＝sin q －cos q －sin q ＋cos q ，
因为q （，），得sin q ＜cos q ＜0，
所以，原式＝cos q －sin q＋sin q ＋cos q ＝2 cos q ．
【答案】（B）．
【点评】
本题考查函数的概念，三角函数值符号、二倍角公式以及三角函数恒等变形的能力．
7．已知sin a
＝
，a （，p），tan（p－b）＝
，则tan（a －2b ）的值等于（ ）．
（A）
（B）－ （C）
（D）－
【提示】
由sin a ＝，a ∈（，p），得cos a ＝－
，tan a ＝－
．
又tan（p－b）＝，得tan b ＝－，tan 2b ＝
＝－
．
所以，tan（a －2b ）＝
＝．
【答案】（A）．
【点评】
本题考查同角三角函数的关系，诱导公式、二倍角的正切公式，两角差的正切公式以及运算能力．
8．要得到函数y＝cos（
－
），x∈R的图象，只需将函数y＝
，x∈R的图象（ ）．
（A）向左平行移动个单位长度
（B）向右平行移动个单位长度
（C）向左平行移动个单位长度
（D）向右平行移动个单位长度
【提示】
由y＝cos（－
）＝cos（－）＝
＝
＝
【答案】（A）．
【点评】本题考查三角函数的图象和性质．注意：当由函数y＝
的图象得到函数y＝
的图象时，需将函数y＝的图象上的所有点沿x轴平移
个单位长度（当＜0时向左移，当＞0时向右移）．
9．适合tan（2x＋
）＝
，x∈
的x值的个数是（ ）．
（A）2 （B）3 （C）4 （D）5
【提示】
由tan（2x＋）＝，得2x＋＝kp
＋
（k∈Z），即x＝kp
－
（k∈Z），满足x∈时，k可取1，2，3，4，故x的值为
，
，
，
共4个值．
【答案】（C）．
【点评】本题考查反正切函数的定义．
10．若0＜a
＜，则arcsin[cos（＋a
）]＋arccos[sin（p＋a
）]等于（ ）．
（A） （B）－ （C）－2a （D）－－2a
【提示】 用特殊值法，由0＜a ＜，取a
＝，
则原式＝arcsin（－
）＋arccos（－）＝－＋
＝．
【答案】（A）．
【点评】本题主要考查反正弦、反余弦的定义及解决问题的能力．
（二）填空题（每题4分，共20分）
1．若角a 的顶点与原点重合，其始边与x轴的非负半轴重合，角a 的平分线过点（－p，p ），那么sin a ＝________，cos a ＝___________．
【提示】角a 的终边与y轴的非正半轴重合，即a ＝＋2kp（k∈R）．
【答案】－1，0
【点评】本题考查三角函数的定义．
2．函数y＝
的值域为__________．
【提示一】化原函数为sin x＝
，由sin x
1，得－11，解之得－y1．
【提示二】运用“分离常数法”．y＝
＝－1＋
，当sin x＝－1时，函数的最小值为－；当x＝1时，最大值为1．
【答案】[－，1]．
【点评】本题考查三角函数的值域及其应用．
3．对于正整数n，f（n）＝sin n a ＋cos n a ，若已知f（1）＝a（ sin a ＋cos a ），
则f（3）＝____________．
【提示】
f（1）＝sin a ＋cos a ＝a，于是，得sin a cos a＝
，
从而f（3）＝sin3 a
＋cos3 a ＝a（1－）＝
．
【答案】．
4．已知＜b
＜a ＜，cos（a －b ）＝
，sin（a ＋b
）＝－，则sin 2a 的值为____．
【提示】
由＜b
＜a ＜，得0 ＜a
－b
＜，p ＜a
＋b ＜，根据cos（a －b ）＝，有sin（a －b ）＝
；根据sin（a ＋b
）＝－，有cos（a ＋b
）＝－，
所以，sin 2a ＝sin[（a －b ）＋（a ＋b）]
＝sin（a －b ）cos（a ＋b ）＋cos（a －b ）sin（a ＋b ）
＝×（－）＋（）×（－）＝－
．
【答案】－．
【点评】
本题考查三角函数的和角公式、同角三角函数关系及运算能力．解题中运用了角的变换，注意到（a ＋b ）＋（a －b ）＝2a ，得sin 2a ＝sin[（a ＋b ）＋（a －b）]，用两角和的正弦公式就可以得出sin 2a 的值，变换的思想是数学的基本思想．
5．函数y＝
是减函数的区间为__________．
【提示】由y＝＝
＝1＋
．
利用对数函数的定义域，知sin 2x＞0，得x∈（kp ，kp＋）（k∈Z）．又y＝sin 2x的递增区间为[－＋kp ，＋kp]（k∈Z），而y＝sin 2x的递增区间即为原函数的递减区间．
所以，原函数的递减区间为（kp ，kp＋）（k∈Z）．
【答案】 （kp ，kp＋）（k∈Z）．
【点评】
本题考查三角函数、对数函数的单调性及复合函数的单调性判断方法．
（三）解答题（每题10分，共50分）
1．求值
．
【提示】“切化弦”后，利用三角函数基础知识，可解．
【答案】
原式＝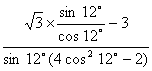
＝ 
＝
＝
＝－
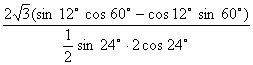
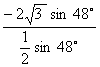
【点评】本题考查灵活运用同角三角函数关系、两角差的正弦、二倍角公式及运算能力．
2．已知0＜b
＜，＜a
＜，cos（－a
）＝，sin（＋b
）＝，
求sin（a ＋b ）的值．
【提示】
用已知角表示所求角，注意到（＋b
）－（－a
）＝＋（a
＋b ），
于是sin（a ＋b
）＝－cos[＋（a
＋b ）]＝－cos[（＋b
）－（－a
）]，
只要求出sin（－a
），cos（＋b
）就可以了．
【答案】
∵ 0＜b
＜，＜a
＜，
∴ －＜－a
＜0，＜＋b
＜p．
由cos（－a
）＝，得sin（－a
）＝－．
由sin（＋b
）＝，得cos（＋b
）＝－．
∴ sin（a
＋b ）＝－cos[＋（a
＋b ）]
＝－cos[（＋b
）－（－a
）]
＝－ cos（＋b
）cos（－a
）－sin（＋b
）sin（－a
）
＝―（―）×―×（―）
＝
【点评】本题考查同角三角函数关系，诱导公式、两角差的余弦公式的灵活运用，考查计算推理能力以及变换的思想．
3．已知△ABC的三个内角A、B、C满足A＋C＝2B，且
＝
，
求
的值．
【提示】由题设A＋C＝2B，可得B＝60°，考虑把当作未知数，通过三角函数式的恒等变形，得到关于的一元二次方程解出即可．
【答案】
∵ 在△ABC中，A＋C＝2B，
∴ B＝60°，A＋C＝120°，
令
＝q
，
则由
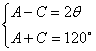得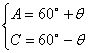 
于是，
＝
＝
＝
＝
又 －＝－
＝－
．
∵ ＝－，
∴ ＝－，
即
＝0 ，
＝0，
∵ 
0，
∴ 
＝0，cos q
＝，
所以，＝．
【点评】
本题综合考查三角函数的基础知识，考查灵活运用三角公式进行恒等变形运算的能力．
4．已知sin 2a ＝，（－＜a
＜p )，函数f (x)＝sin（a
－
x）－sin（a ＋x）＋2 cos a 有最大值0 ，求当x为何值时，f (x)有最小值？最小值是多少？
【提示】
化简函数式，得f (x)＝2 cos a（1－sin x）．根据题意，计算出cos a 的值，再利用
sin x 1，就可以求出f (x)的最小值．
【答案】
∵ f (x)＝sin（a －x）－sin（a ＋x）＋2 cos a
＝sin a cos x－cos a sin x－sin a cos x－cos a sin x＋2 cos a
＝2 cos a －2 cos a sin x
＝2 cos a（1－sin x）
又f (x)≤0，
∴ 2 cos a（1－sin x）≤0，
而1－sin x≥0，
∴ cos a ＜0，
∵ －＜a
＜p ，
于是－＜a
＜－ 或＜a
＜p，－＜2a ＜－p，或p ＜2a
＜2p ．
又sin 2a ＝＞0，
∴ －＜2a ＜－p，且cos 2a ＝－．
也就是2 cos 2 a ＝－，即cos a ＝－
．
∴ f (x) ＝－
，
当sin x＝－1时，即x＝2 kp－（k
Z）时，f (x)有最小值－
．
【点评】
本题综合考查三角函数的基础知识（两角和差的正弦公式、同角三角函数关系、二倍角公式、函数的最值等）以及运算能力．
5．记函数f (x) ＝1－2a－2acos x－2 sin2 x的最小值为f（a）．
（1）写出函数f（a）的表达式；
（2）若f（a）＝，求这时函数f（a）的最大值．
【提示】
化简函数式，得f (x) ＝
，由 cos x 1，利用二次函数的图象性质，应分情况讨论．
【答案】
（1）∵ f (x) ＝1－2a－2a cos x－2 sin2 x
＝1－2a－2a cos x－2(1－cos2 x)
＝2 cos2 x－2a cos x－2a－1
＝．
又 cos x 1，
①当－1
1，即－2a2时，取cos x＝，f（a）＝
；
②当＞1，即a＞2时，取cos x＝1，f（a）＝
＝1－4a；
③当＜－1，即a＜－2 时，即cos x＝－1，f（a）＝
＝1．
综上，有 f（a）＝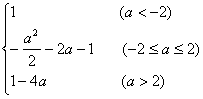
．
（2）若f（a）＝，显然a
－2．
①当－2a2时，＝，即a2 ＋4a＋3＝0，a＝－1或a＝－3（舍去），
②当a＞2时，1－4a＝，即a＝
（舍去）．
于是，满足f（a）＝，a＝－1，此时，f（x）＝
，当cos a ＝1时，
f max（x）＝
＝5．
【点评】
本题综合二次函数的图象性质，考查与三角函数有关的函数最大（小）值的问题，考查灵活运用所学知识分析问题、解决问题的能力，以及数形结合、分类讨论、转化等数学思想方法．