提高测试（一）
（一）选择题（每题3分，共30分）
1．下列命题中，真命题是（ ）．
（A）若sin a＞0，则
（B）若sin a＞0，则cos a＞0
（C）若tan a＞0，则sin 2a ＞0
（D）若cos a ＜0，则cos 2a＜0
【提示】根据三角函数值的符号，确定角a 所在的象限，再由角
，2 a 所在的象限，判断相应三角函数值的符号．
【答案】（C）．
【点评】
本题考查三角函值的符号．由sin a ＞0，得2kp＜a
＜2kp＋p（k
Z），于是
kp＜＜kp＋
（kZ），知是第一或第三象限角，故排除（A）．
由sin a＞0，得a 是第一或第二象限角，排除（B）．
由cos a ＜0，得2kp＋＜a ＜2kp＋
（kZ），于是4kp＋p＜2a ＜4kp＋3p （kZ），此时，2a
可能是任何象限的角，排除（D）．
而由tan a＞0，知kp＜a ＜kp＋（kZ），于是2kp＜2a ＜2kp＋p，此时sin 2a ＞0成立．
2．若f（cos x）＝cos 2x，则f（sin 15°）的值是（ ）．
（A）
（B）
（C）－ （D）－
【提示一】
由f（cos x）＝cos 2x＝2 cos2 x－1，得f（x）＝2x2－1，于是
f（sin 15°）＝2 (sin 15°)2－1＝―cos30°＝―．
【提示二】
f（sin 15°）＝f（cos 75°）＝cos 150°＝―cos30°＝―．
【答案】（D）．
【点评】本题结合函数的概念考查二倍角公式或诱导公式的灵活应用．
3．下列函数中，周期为的偶函数是（ ）．
（A）f（x）＝sin 4x，x∈R
（B）f（x）＝cos2 2x－sin2 2x， x∈R
（C）f（x）＝tan 2x，x∈R且x
＋
（k∈Z）
（D）f（x）＝cos 2x，x∈R
【提示】
（A）、（C）中的函数为奇函数，（D）中的函数周期是p
，而对于（B），f（x）＝cos 4x 是周期为的偶函数．
【答案】（B）．
【点评】本题考查三角函数的奇偶性、周期性和二倍角公式．
4．比较
，
，－
的大小顺序是（ ）．
（A）＜＜－
（B）＜－＜
（C）＜＜－
（D）－＜＜
【提示】
cos 86°，sin 5.7°＝cos 84.3°，－－cos100.3°＝cos 79.7°，而y＝cos x在（0，
）为减函数，得
cos 86°＜cos 84.3°＜cos 79.7°，即＜＜－．
【答案】（A）．
【点评】本题考查诱导公式及余弦函数的单调性．在比较大小时，一般是先将各三角函数都化为同名的三角函数，再将各角化为第一象限的角，最后利用三角函数的单调性来比较．
5．要使sin a －
cos a ＝
有意义，m的取值范围是（ ）．
（A）[－1，0] （B）[0，
] （C）[－1，] （D）[
，4]
【提示】
由于sin a － cos a ＝2sin（a －
），得－2
2 ，解不等式，得
m∈[－1，]．
【答案】（C）．
【点评】本题考查两角差的正弦，三角函数的值域以及解不等式的有关知识．
6．在直角三角形中两锐角为A和B，则sin A sin B（ ）．
（A）有最大值和最小值0
（B）有最大值，但无最小值
（C）既无最大值也无最小值
（D）有最大值1，但无最小值
【提示】
因为A＋Ｂ＝90°，有sin A sin B＝sin A cos A＝ sin 2A．又0°＜A＜90°，所以当
A＝45°时，sin A sin B有最大值，但2A∈(0，180°)，sin 2A无最小值．
【答案】（B）．
【点评】本题考查三角函数的诱导公式及二倍角的正弦公式、正弦函数的有界性等知识．
7．函数y＝A sin（w x＋j）在同一区间内，当x＝
时，y取得最大值；当x＝
时，y取得最小值－，则函数的解析式是（ ）．
（A）y＝ sin（
－
）
（B）y＝ sin（3x＋）
（C）y＝ sin（＋）
（D）y＝ sin（3x－）
【提示】
显然A＝，
＝－
＝，T ＝
．则w
＝
＝3，将（，）代入
y＝ sin（3x＋j），得j ＝，于是y＝ sin（3x＋）．
【答案】（B）．
【点评】本题考查三角函数y＝ A sin（w x＋j）的图象和性质．
8．下列各式中正确的是（ ）．
（A）arcsin（－）＝－
（B）arcsin（sin
）＝－
（C）arcsin（arcsin）＝
（D）sin[arccos（－）]＝－
【提示】利用反正弦函数、反余弦函数的定义．
【答案】（B）．
【点评】本题考查反正弦、反余弦的定义．对于arcsin x＝a ，x表示角a的正弦值，且 x 1，而－＜－1，排除（A）；又＞1，排除（C）；由于arccos（－）＝，sin ＝，排除（D）．而sin ＝－
，arcsin（－）＝－．故选（B）．
9．使函数y＝sin（2x＋q ）＋ cos（2x＋q ）为奇函数，且在[0，]上是减函数的q 的一个值是（ ）．
（A） （B） （C）
（D）
【提示】
由于y＝2 sin（2x＋q
＋）为奇函数，再将各选项的q 的值逐项代入，可排除（A）、（C）．又x∈[0，] 时原函数为减函数，再排除（D）．
【答案】（B）．
【点评】本题考查两角和的正弦公式、函数的奇偶性以及函数的单调性．
10．已知tan a ，tan b 是方程x2＋
x＋4＝0的两根，且－＜a
＜，－＜b
＜，则a
＋b 等于（ ）．
（A） （B）－ （C）或 （D）－或
【提示】
因为tan a ＋tan b ＝－，tan a tan b ＝4，则tan（a＋b ）＝
＝．同时由tan a ＋tan b
＜0，tan a tan b
＞0，可知tan a ，tan b
均小于零， 故a 、b
（－，0），所以a ＋b
（－p ，0），得a ＋b ＝－．
【答案】（B）．
【点评】本题考查两角和的正切公式，以及综合运用韦达定理解决问题的能力．
（二）填空题（每题4分，共20分）
1．函数y＝
的周期T ＝_______．
【提示一】
y＝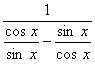
＝
＝
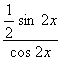＝ tan 2x．
【提示二】
y＝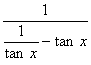
＝
＝ tan 2 x．
【答案】
【点评】本题考查同角三角函数关系，二倍角公式及正切函数的周期性．
2．求
的值等于________．
【提示】
＝
＝
＝
＝
＝
＝
．
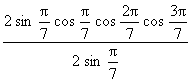
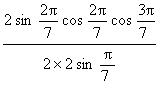
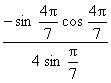
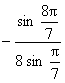
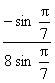【答案】．
【点评】本题考查二倍角公式及诱导公式以及三角恒等变形的能力．
3．函数y＝
＋
在（－2p，2p）内的递增区间是_____________．
【提示】
y＝＋＝
，函数y的单调递增区间由下面的条件决定：
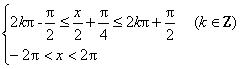
解之即可．
【答案】[－，]．
【点评】本题考查三角函数式的恒等变形及三角函数的单调性．
4．函数f（x），xR是奇函数，且当x
0时，f（x）＝x2＋sin x，则当x＜0时，f（x）＝____________．
【提示】
当x＜0时，－x＞0，由题设f（－x）＝（－x）2＋sin（－x）＝x2－sin x.，又f（x）为奇函数，f（－x）＝－f（x），于是f（x）＝－f（－x）＝－x2＋sin x．
【答案】－x2＋sin x．
【点评】本题考查函数的概念，函数的奇偶性及运算能力．
5．方程＝
在[p，2p]上的解是___________．
【提示】
由＝，得
＝kp＋（－1）k
，x＝2kp＋（－1）k
（kZ），当k＝1时，有x＝2p－[p，2p]．
【答案】2p－．
【点评】本题考查反正弦的定义．
（三）解答题（每题10分，共50分）
1．已知角a 的顶点与直角坐标系的原点重合，始边在x轴的非负半轴上，终边经过
点P（－１，2），求sin（2a ＋）的值．
【提示】画出图形，先求得sin a ，cos a 的值．
【答案】据已知， OP ＝
＝
，
由三角函数的定义，sin a ＝
，cos a ＝－
．
于是，sin 2a ＝2 sin a
cos a ＝－
， cos 2a ＝2 cos2 a
－1＝－
．
∴ sin（2a ＋）＝
＋
＝－×（－）＋（－）×
＝
．
【点评】本题考查三角函数的定义，两角和的正弦、倍角公式及计算能力．
2．设p＜A＜，0＜B＜，且cos A＝－
，cot B＝3，求证A－B＝
．
【提示】根据已知，先计算tan（A－B）的值，再判断A－B的取值范围．
【答案】∵ p＜A＜，cos A＝－，
∴ sin A＝－
＝
，
于是，tan A＝
＝2．
又cot B＝3，得tan B＝．
∴ tan（A－B）＝
＝
＝1．
∵ p＜A＜，0＜B＜，
∴ ＜A－B＜．
∴ A－B＝
．
【点评】本题考查同角三角函数间的关系，两角差的正切，由三角函数值确定角的方法．
3．已知cos a ＝cos x·sin g ，cos b ＝sin x·sin g ，求证sin2 a ＋sin2 b ＋sin2 g ＝2
【提示】 利用已知条件，注意到sin2 a ＝1－cos2 a ，sin2 b ＝1－cos2 b ，将条件代入原式的左边，化简即可．
【答案】左边＝1－cos2 a ＋1－cos2 b ＋sin2 g
＝2－cos2 a －cos2 b ＋sin2 g ，
又cos a ＝cos x sin g ，cos b ＝sin x sin g ，
∴ 左边＝2－cos2 x sin2 g －sin2 x sin2 g ＋sin2 g
＝2－sin2 g（sin2 x＋cos2 x）＋sin2 g
＝2－sin2 g＋sin2 g
＝2
∴ 原结论成立．
【点评】
本题通过三角恒等式的证明，考查三角函数恒等变形能力．寻求已知条件与所证恒等式之间的关系是证明的关键．
4．已知函数y＝
＋
＋1，xR
（1）当函数y取得最大值时，求自变量x的集合；
（2）该函数的图象可由y＝sin x，xR的图象经过怎样的平移和伸缩变换得到？
【提示】利用三角函数的有关公式，对函数y进行化简．
【答案】 （1）y＝＋＋1
＝
（2 cos2 x－1）＋
（2 sin x cos x）＋＋1
＝
＝
＝
．
当y取最大值时，必须有2x＋＝2kp＋，即x＝kp＋（kZ）．
∴ 当函数y取得最大值时，自变量x的集合为 x{x＝kp＋，kZ}．
（2）【解法一】将函数y＝sin x依次进行如下变换：
①把函数y＝sin x的图象向左平行移动个单位长度，得到函数y＝sin（x＋）的图象；
②把所得图象上各点的横坐标缩短到原来的倍（纵坐标不变），得到函数
y＝sin（2x＋）的图象；
③把得到的图象上的各点的纵坐标缩短到原来的倍（横坐标不变），得到函数
y＝
的图象；
④把得到的图象向上平行移动
个单位长度，得到函数y＝的图象．
综上得到函数y＝＋＋1的图象．
【解法二】
①把函数y＝sin x图象上所有的点的横坐标缩短为原来的倍（纵坐标不变），得到函数y＝sin 2x的图象；
②再将图象上所有的点向左平行移动
个单位长度，得函数y＝
的图象；③将得到的图象上的所有点的纵坐标缩短为原来的倍（横坐标不变），得到函数
y＝的图象；
④将得到的图象向上平行移动个单位长度，得函数y＝的图象．
【点评】
本题是2000年高考题，主要考查三角函数的图象和性质，考查利用三角公式进行恒等变形的技能以及运算能力．注意：在由y＝sin x的图象得到y＝sin w x的图象时，是把y＝sin x的图象上所有点的横坐标伸长（或缩短）到原来的
倍（纵坐标不变），而不是w
倍．
5．设函数y＝sin 2
x＋a cos x＋
a－在0x上的最大值为1，求a的值．
【提示】
将函数y变形为y＝－（cos x－
）2＋
＋a－，由cos x [0，1]，利用二次函数的图象性质，分情况讨论．
【答案】
∵ y＝sin 2
x＋a cos x＋a－
＝1－cos 2 x＋a cos x＋a－
＝－（cos x－）2＋＋a－．
由0x，得0cos x1．
下面对a的取值情况分类讨论：
（1）当0a2时，函数y在cos x＝处取得最大值＋a－，据已知，
＋a－＝1，即2a2＋5a－12＝0，得a＝或a＝－4（舍去）；
（2）当a＜0时，函数y在cos x＝0时取得最大值a －，有a －＝1，
即a＝
（舍去）；
（3）当a＞2时，函数y在cos x＝1处取得最大值
，有＝1，
即a ＝
（舍去）．
∴ a ＝即为所求．
【点评】本题通过三角函数的有界性，结合二次函数的性质考查在限定区间内函数的最大（小）值的问题，以及综合运用数学知识解决问题的能力．