高一（上）数学单元同步练习
第五单元 对数与对数函数
[重点难点]
1． 理解对数的概念，能够进行对数式与指数式的互化；掌握对数的运算性质，能够熟练应用对数运算性质进行计算或证明；了解常用对数和自然对数的概念。
2． 掌握对数函数的概念，并能求出对数函数的定义域和值域。
3． 能根据互为反函数的两个函数图像间的关系，利用指数函数的图像，描绘出相应的对数函数的图像。
4． 能根据对数函数的图像归纳出对数函数在底数a>1和0<a<1两种情况下所具有的一些重要性质；并能利用对数函数的性质，求某些函数的定义域和比较某些函数值的大小。
一、 选择题
1．若3a=2,则log38-2log36用a的代数式可表示为（ ）
（A）a-2 （B）3a-(1+a)2 （C）5a-2 （D）3a-a2
2.2loga(M-2N)=logaM+logaN,则
的值为（ ）
（A）
（B）4 （C）1 （D）4或1
3．已知x2+y2=1,x>0,y>0,且loga(1+x)=m,loga
等于（ ）
（A）m+n （B）m-n （C）
(m+n) （D）(m-n)
4.如果方程lg2x+(lg5+lg7)lgx+lg5·lg7=0的两根是α、β，则α·β的值是（ ）
（A）lg5·lg7 （B）lg35 （C）35 （D）
5.已知log7[log3(log2x)]=0，那么x
等于（ ）
（A）
（B）
（C）
（D）
6．函数y=lg（
）的图像关于（ ）
（A）x轴对称 （B）y轴对称 （C）原点对称 （D）直线y=x对称
7．函数y=log2x-1
的定义域是（ ）
（A）（
，1）
（1，+
） （B）（，1）（1，+）
（C）（，+）
（D）（，+）
8．函数y=log
(x2-6x+17)的值域是（ ）
（A）R
（B）[8，+]
（C）（-，-3）
（D）[3，+]
9．函数y=log(2x2-3x+1)的递减区间为（ ）
（A）（1，+）
（B）（-，
］
（C）（，+）
（D）（-，］
10．函数y=()
+1+2,(x<0)的反函数为（ ）
（A）y=-
（B）
（C）y=-
（D）y=-
11.若logm9<logn9<0,那么m,n满足的条件是（ ）
（A）m>n>1 （B）n>m>1
（C）0<n<m<1 （D）0<m<n<1
12.loga
，则a的取值范围是（ ）
（A）（0，）（1，+）
（B）（，+）
（C）（
）
（D）（0，）（，+）
13．若1<x<b,a=log２bx,c=logax,则a,b,c的关系是（ ）
（A）a<b<c （B）a<c<b （C）c<b<a （D）c<a<b
14.下列函数中，在（0，2）上为增函数的是（ ）
（A）y=log(x+1)
（B）y=log2
（C）y=log2
（D）y=log
(x2-4x+5)
15.下列函数中，同时满足：有反函数，是奇函数，定义域和值域相同的函数是（ ）
（A）y=
（B）y=lg
（C）y=-x3
（D）y=
16.已知函数y=loga(2-ax)在[0，1]上是x的减函数，则a的取值范围是（ ）
（A）（0，1） （B）（1，2） （C）（0，2） （D）[2，+)
17．已知g(x)=loga
(a>0且a
1)在（-1，0）上有g(x)>0，则f(x)=a
是（ ）
（A）在（-，0）上的增函数
（B）在（-，0）上的减函数
（C）在（-，-1）上的增函数
（D）在（-，-1）上的减函数
18．若0<a<1,b>1,则M=ab，N=logba,p=ba的大小是（ ）
（A）M<N<P （B）N<M<P
（C）P<M<N （D）P<N<M
19．“等式log3x2=2成立”是“等式log3x=1成立”的（ ）
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）既不充分也不必要条件
20．已知函数f(x)=
,0<a<b,且f(a)>f(b)，则（ ）
（A）ab>1 （B）ab<1 （C）ab=1 （D）(a-1)(b-1)>0
二、填空题
1．若loga2=m,loga3=n,a2m+n= 。
2．函数y=log(x-1)(3-x)的定义域是 。
3．lg25+lg2lg50+(lg2)2= 。
4.函数f(x)=lg(
)是
（奇、偶）函数。
5．已知函数f(x)=log0.5 (-x2+4x+5),则f(3)与f（4）的大小关系为 。
6．函数y=log(x2-5x+17)的值域为
。
7．函数y=lg(ax+1)的定义域为（-，1），则a=
。
8.若函数y=lg[x2+(k+2)x+
]的定义域为R，则k的取值范围是
。
9．函数f(x)=
的反函数是
。
10．已知函数f(x)=()x,又定义在（-1，1）上的奇函数g(x)，当x>0时有g(x)=f-1（x）,则当x<0时，g(x)=
。
三、解答题
1．
若f(x)=1+logx3,g(x)=2log
，试比较f(x)与g(x)的大小。
2．
对于函数f(x)=lg
,若f(
)=1,f(
)=2,其中-1<y<1,-1<z<1,求f(y)和f(z)的值。
3．
已知函数f(x)=
。
（1）判断f(x)的单调性；
（2）求f-1(x)。
4．
已知x满足不等式2(log2x）2-7log2x+3
0,求函数f(x)=log2
的最大值和最小值。
5．
已知函数f(x2-3)=lg
,
(1)f(x)的定义域；
(2)判断f(x)的奇偶性；
(3)求f(x)的反函数;
(4)若f[
]=lgx,求
的值。
6．
设0<x<1,a>0且a1，比较
与
的大小。
7．
已知函数f(x)=log3
的定义域为R，值域为[0，2]，求m,n的值。
8．
已知x>0,y
0,且x+2y=,求g=log (8xy+4y2+1)的最小值。
第五单元 对数与对数函数
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | D | D | C | C | A | C | A | D |
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | C | A | D | D | C | B | C | B | B | B |
二、填空题
1．12 2.{x
且x
} 由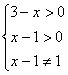
解得1<x<3且x。
3．2
4．奇
为奇函数。
5．f(3)<f(4)
设y=log0.5u,u=-x2+4x+5,由-x2+4x+5>0解得-1<x<5。又
u=-x2+4x+5=-(x-2)2+9,∴ 当x
(-1,2)时，y=log0.5(-x2+4x+5)单调递减；当x[2,5]时，y=log0.5(-x2+4x+5)单调递减，∴f(3)<f(4)
6.(-
) ∵x2-6x+17=(x-3)2+8
,又y=log
单调递减，∴ y
7.-1
8.-
y=lg[x2+(k+2)x+]的定义域为R，∴ x2+(k+2)x+>0恒成立，则
（k+2）2-5<0,即k2+4k-1<0,由此解得-
-2<k<-2
9.y=lg
y=,则10x=
反函数为y=lg
10.-log(-x)
已知f(x)=()x,则f-1(x)=logx,∴当x>0时，g(x)=logx,当x<0时，-x>0, ∴g(-x)
=log(-x),又∵g(x)是奇函数，∴
g(x)=-log(-x)(x<0)
三、解答题
1． f(x)-g(x)=logx3x-logx4=logx
.当0<x<1时，f(x)>g(x);当x=
时，f(x)=g(x);当1<x<时，f(x)<g(x);当x>时，f(x)>g(x)。
2． 已知f(x)=lg
①,又∵f()=lg
②,
①②联立解得
,∴f(y)=
,f(z)=-。
3．（1）f(x)=
，
,且x1<x2,f(x1)-f(x2)=
<0,(∵102x1
<102x2)∴f(x)为增函数。
（2）由y=
得102x=
∵102x>0,
∴-1<y<1,又x=
)。
3． 由2（log2x）2-7log2x+30解得log2x3。∵f(x)=log2
(log2x-2)=(log2x-)2-,∴当log2x=时，f(x)取得最小值-；当log2x=3时，f(x)取得最大值2。
5．（1）∵f(x2-3)=lg
,∴f(x)=lg
,又由
得x2-3>3,∴ f(x)的定义域为（3，+）。
（2）∵f(x)的定义域不关于原点对称，∴ f(x)为非奇非偶函数。
（3）由y=lg
得x=
,x>3,解得y>0, ∴f-1(x)=
(4) ∵f[]=lg
,∴
，解得
(3)=6。
6．∵
-
。
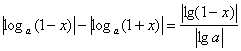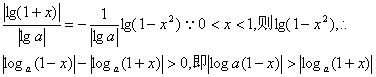7．由y=log3，得3y=
，即（3y-m）x2-8x+3y-n=0. ∵x
-4(3y-m)(3y-n)0，即32y-(m+n)·3y+mn-16
。由0
，得
，由根与系数的关系得
，解得m=n=5。
8．由已知x=-2y>0,
,由g=log
(8xy+4y2+1)=log(-12y2+4y+1)=log[-12(y-
)2+],
当y=,g的最小值为log