第五章《平面向量》提高测试题(二)

提高测试（二）

（一）选择题（每题4分，共24分）

1．设、、是任意的非零平面向量，且相互不共线，则

①（·）－（·）＝；

② －＜－；

③（·）－（·）不与垂直；

④（3＋2）·（3－2）＝9²－4²

中，是真命题的有

（A）①②　　（B）②③　　（C）③④　  （D）②④

【提示】

对于②，、，－表示三角形的三条边长，可得－＜－，故②是正确的，排除（C）；对于④，利用向量的运算，可得④正确的．

【答案】（D）．

【点评】

本题考查平面向量中零向量、共线向量、向量的垂直、向量的横等有关概念和向量的加、减、与实数的积，数量积这些基本的运算及其运算性质．因为向量的数量积不满足结合律，即（·）·≠·（·），故命题①是错误的；而对于[（·）－（·）]·＝（·）·－（·）·＝0，有（·）－（·）与是垂直的，故命题③是错误的．

2．已知向量＝1，0），＝（0，1），则与2＋垂直的向量是（　　）．

（A）2－　　（B）－2

（C）2＋　　（D）＋2

【提示一】

利用向量的坐标计算

∵　＝（1，0），＝（0，1），

∴　2＋＝（2，1）

而－2＝（1，－2）

有（2＋）（－2）＝2×1＋（－2）×1＝0，

∴　（2＋）⊥（－2）．

【提示二】

利用向量的运算

由已知，得＝1，＝1，·＝0，

∴　（2＋）（－2）＝2－3·－2＝0，

∴　（2＋）⊥（－2）．

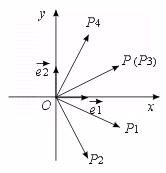
【提示三】

利用向量的几何意义．由已知，可得与是互相垂直的单位向量．

如图，在直角坐标系中，2＋＝．

显然　2－表示的向量不与垂直，2＋表示的向量与重合；＋2表示的向量也不与垂直．

【答案】（B）．

【点评】

本题主要考查向量垂直的充要条件．通常有三种方法，一是利用向量的坐标运算；二是利用向量的运算，三是利用向量的几何意义．

3．已知＝（－2，3），＝（3，2），若m₁＝·，m₂＝·（＋），m₃＝（＋），m₄＝（＋）（－），m₅＝(＋)²，则m₁，m₂，m₃，m₄，m₅的大小顺序是（　　）．

（A）m₁＜m₂＝m₃＜m₄＜m₅

（B）m₁＜m₃＝m₄＜m₂＜m₅

（C）m₁＝m₄＜m₂＝m₃＜m₅

（D）m₁＝m₅＜m₄＝m₂＜m₃

【提示】

利用向量的坐标运算，分别计算出m₁＝（－2）×3＋3×2＝0，m₂＝（－2）×1＋3×5＝13，m₃＝3×1＋2×5＝13，m₄＝1×（－5）＋5×1＝0，m₅＝26，于是m₁＝m₄＜m₂＝m₃＜m₅．

【答案】（C）．

【点评】本题主要考查向量的坐标运算及计算能力．

4．已知向量与不共线，＝＋k，＝l＋（k，l∈R），则与共线的条件是（　　）．

（A）k ＋l ＝0　　 （B）k －l ＝0

（C）kl＋1＝0　　  （D）kl－1＝0

【提示】

∵　∥，

∴　＋k＝l（l＋）　（l∈R）

即　（1－ll）＋（k －l）＝

∵　、不共线，则

，消去l，

∴　kl－1＝0．

【答案】（D）．

【点评】

本题考查向量共线的充要条件、向量相等的充要条件及逻辑推理能力．即引入l后，再设法消去l，寻求k与l的关系式．

5．设，，为平面上的三个向量，且满足＝，＝，·＝（k ＝1，2），则能使a＋b＝成立的常数a、b的值是（　　）．

（A）a ＝6，b ＝6　　 （B）a ＝－6，b ＝6

（C）a ＝6，b ＝－6　 （D）a ＝－6，b ＝－6

【提示】要求a、b的值，必需寻求含有a、b的两个关系式．

由已知，得

·＝1，·＝，·＝，

²＝，²＝．

对于a＋b＝，

等式两边同乘以，得

a²＋b·＝·，

即　a ＋b ＝1．　　①

等式两边同乘以，得

a·＋b²＝·，

即　a ＋b ＝．　　②

由①、②，可得

a ＝6，b ＝－6．

【答案】（C）．

【点评】本题考查平面向量的数量积及运算律，考查方程的思想方法及逻辑推理能力．

6．在四边形ABCD中，E是AB的中点，K是CD的中点，则以线段AK，CE，BK，DE的中点为顶点的四边形是（　　）．

（A）任意四边形　　（B）平行四边形

（C）矩形　　　　  （D）菱形

【提示一】利用坐标法．

设A（a₁，a₂），B（b₁，b₂），C（c₁，c₂），D（d₁，d₂），则K（，），

E（，），

若AK，BK，CE，DE的中点分别为O₁，O₂，O₃，O₄，则

O₁，O₂，O₃，O₄，则

O₁（，），O₂（，），

O₃（，），O₄（，）．

于是，

O₁O₂的中点坐标为（，），

O₃O₄的中点坐标为（，）．

∴　四边形O₁O₄O₂O₃为平行四边形．

利用向量的坐标运算，可进一步验证·≠0，排除（C）；·≠0，排除（D）．

【提示二】利用向量式

若AK，BK，CE，DE的中点分别为O₁，O₂，O₃，O₄，则

＝（＋），＝（＋），

＝＝（＋），

＝＝（＋）．

∴　＝－

＝[（＋）－（＋）]

＝（－）

＝[（＋＋）－]

＝（＋）

＝[（）＋（）]

＝（＋）．

又　＝－

＝[（＋）－（＋）]

＝（－）

＝[－（＋＋）]

＝（－－）

＝[（）＋（）]

＝（＋）．

∴　＝，即四边形O₁O₄O₂O₃是平行四边形．

【答案】（B）．

【点评】本题主要考查了向量的运算，提示一利用向量的坐标表示及线段的中点坐标公式．将平面几何图形的位置关系转化为坐标的计算问题；提示二利用向量的加、减法运算律，线段中点的向量形式，将问题转化为向量的线性运算，这正体现了向量工具的重要作用之一．

（二）填空题（每题4分，共20分）

1．已知平行四边形ABCD的三个顶点A（0，0），B（3，1），C（4，1），则D点的坐标为__________．

【提示】设D（x，y），在□ABCD中，由＝，得

（4－x，3－y）＝（3，1）

∴　即

【提示二】

设点O为□ABCD中两条对角线AC、BD的交点．

∵　A（O，O），C（4，3），且O为AC的中点，

∴　O（2，）．

又　O为BD的中点，B（3，1），

∴　D（1，2）．

【答案】（1，2）．

【点评】本题考查向量的基础知识及其运算．

求点的坐标的基本方法有两种，一是利用向量的坐标运算，本题提示一利用了相等向量的定义，也可由＝，求得点D的坐标；二是利用线段的定比分点的坐标公式，提示二的解法利用了中点坐标公式．

2．已知＝（m ＋1，－3），＝（1，m －1），且（＋）⊥（－），则m的值是__________．

【提示】先由向量、的坐标，求得＋＝（m ＋2，m －4），－＝（m，－2－m），再利用向量垂直的充要条件，得（＋）·（－）＝0，即

（m ＋2）×m＋（m －4）×（－2－m）＝0，

解出　m ＝－2．

【答案】－2．

【点评】本题考查向量的坐标运算，向量垂直的充要条件及计算能力．

3．将函数y ＝log₃（2 x ＋1）－4的图象按向量平移后得到的是函数y ＝log₃^2x的图象，则的坐标是___________．

【提示】设平移向量＝（h，k）．

由平移公式　即

把（x，y）代入y ＝log₃（2 x ＋1）－4中，得

y′－k ＝log₃[2（x′－h）＋1]－4，

即　y′＝log₃[2 x′＋（1－2 h）]＋（k －4）．

∵　平移后得到的是函数　y ＝log₃^2x的图象，

∴　　　即

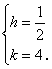
∴　＝（，4）．

【点评】利用平移可以将复杂函数式转化为简单函数式，这是研究函数的一种重要方法．

4．若向量＝（，－1），＝（，），＝＋（x²－3），＝－y＋x，且x³－3 x －4 y ＝0，则与的夹角等于________．

【提示】要求与的夹角，可通过·来解．据已知，

·＝－y²＋x（x²－3）²＋[x －y（x²－3）] ·．

又　²＝4，²＝1，

·＝×＋（－1）×＝0．

∴　·＝－4 y ＋x³－3 x

＝（x³－3 x）＋x³－3 x

＝0．

∴　⊥，即与的夹角为90°．

【答案】90°．

【点评】本题主要考查向量的数量积及运算律．考查计算及逻辑推理能力．

5．求值：sin ² 20°＋cos ² 80°＋sin 20°cos 80°＝_________．

【提示】

分析原式的结构特点，联想到余弦定理．将其转化为边长的形式，构造三角形可求得原式的值．

【解】由于　cos 80°＝sin 10°，则

sin²20＋cos²80°＋sin 20°cos 80°

＝sin ²20°＋sin²10°＋sin 20°sin 10°．

构造△ABC，使A ＝20°，B ＝10°，C ＝150°，三角形的外接圆半径为R．

则由正弦定理，得a ＝2 R sin A，b ＝2 R sin B，c ＝2 R sin C．

再据余弦定理，有c²＝a²＋b²－2 ab cos C，

(2 R sin C)²＝(2 R sin A)²＋(2 R sin B)²－2 (2 R sin A) (2 R sin B) cos C．

即　sin² C ＝sin² A ＋sin² B －2 sin A sin B cos C．

sin ² 150°＝sin²20°＋sin²10°－2 sin 20°sin 10°cos 150°．

∴　sin² 20°＋cos² 80°＋sin 20°cos 80°＝．

【点评】

本题的解法很多，常用的方法是逆用倍角公式，由 sin²20°＝，cos²80°＝，然后再利用和差化积，积化和差公式，两角和差的三角函数式来化简，一般解题过程较长．前面提供的解法可以说另辟蹊径，据已知三角形函数式结特点，构造三角形，借用余弦定理求解思路新奇，简捷明快．

（三）解答题（每题14分，共56分）

1．在△ABC中，A ＝120°，sin B ∶ sin C ＝3︰2，S_△ABC＝6，求a．

【提示】

在△ABC中，要求a的值，已知A，应用余弦定理，只需求得b，c的长．由sin B∶sin C ＝3∶2，应用正弦定理，可将角的关系转化为b、c边的关系，再利用面积公式，得b、c的另一个关系式，解关于b、c的二元方程组，即可．

【答案】

在△ABC中，由正弦定理，得

＝＝．　 ①

又S_△ABC＝bc sin A ＝bc sin 120°＝6，

于是，bc ＝24．　　②

由①、②，可得b ＝6，c ＝4．（负值舍去）

据余弦定理，得

a²＝b²＋c²－2 bc cos A

＝36＋16－2×6×4×cos 120°

＝76，

∴　a ＝2．

【点评】

本题考查应用正弦定理、余弦定理解斜三角形的有关知识．在解三角形时，常常要将正弦定理，余弦定理交替使用，尽管有时不是直接求出结果，但为了过渡，也是很有必要的．

2．如图，在四边ABCD中，BC ＝a，DC ＝2 a，四个内角A、B、C、D的度数的比为

3︰7︰4︰10，求AB的长．

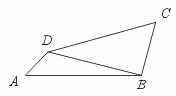
【提示】

由于AB在△ABD中，寻求使△ABD有解的条件是关键，据四边形内角和为360°及四个内角之比，可求得四个内角．此时△BDC便是已知两边BC、DC及夹角C．于是这个三角形可解．借助△BDC可以求的BD，∠ACB用正弦定理可得AB．

【解】连BD，设四个角A、B、C、D的度数分别为3 x，7 x，4 x，10 x．则由四边形内角和，有3 x ＋7 x ＋4 x ＋10 x ＝360°

∴　x ＝15°．

∴　A ＝45°，B ＝105°，C ＝60°，D ＝150°．

在△BCD中，由余弦定理，得

BD²＝BC²＋CD²－2 BC · CD cos C

＝a ²＋4 a ²－2 a · 2 a ·

＝3 a²．

∴　BD ＝a．

这时有，BD²＋BC²＝DC²，则△BDC为直角三角形，∠DBC ＝90°．

∴　∠CDB ＝30°．

于是　∠ADB ＝120°．

在△ADB中，由正弦定理，得

AB ＝

＝

＝．

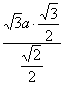
【点评】

本题重点考查正弦定理，余弦定理及解斜三角形的基本方法、题目的已知条件以四边形为背景给出．实际四个内角和两条边已知，去求另外一边AB．一般的思路将所求的边AB放在三角形内，求解这个三角形是问题解决的核心，这就需要根据已知条件寻求解决AB所在三角形的充分条件．该找边的找边、该求角的求角．解决问题过程中，还需注意设计好演算程序，先求谁，后求谁，再求谁．显得思路清晰、演算合理．

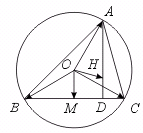
3．设锐角△ABC的外接圆圆心为O，边BC的中点为M，自顶点向BC引垂线，垂足为D，并在垂线上取一点H，与M在AO的同一侧，使得AH ＝2 OM，若＝，＝，＝．

（1）试用、、表示、；

（2）据（1）的结论，证明BH ⊥AC，CH ⊥AB．

【提示】

（1）用、、表示、，即寻求，关于、、的线性分解式，在△BOC中，可得，再利用＝2，而＝＋，得；（2）要证BH ⊥AC，只需证明·＝0，用、、表示，，化简即可，同理可证CH ⊥AB．

【答案】

（1）在△BOC中，M为BC的中点，

∴　＝（＋）＝（＋）．

∵　＝2，

∴　＝＋，

∴　＝－＝＋＝＋＋，

（2）∵　＝＋＝－＋（＋＋）＝＋，

＝＋＝－＋，

∴　·＝（＋）（－＋）＝²－²

又　O为△ABC外接圆的圆心，有

＝＝．

∴　·＝0，即　BH ⊥AC．

同理，＝＋，＝－，

·＝（＋）（－）＝²－²＝0，

∴　CH ⊥AB．

【点评】本题考查向量的加减法及运算律，向量的基本定理及向量垂直的充要条件，考查逻辑推理能力．

4．试证：从任意五个向量中总可以选出两个，使得它们之和的长不超过其余三个向量之和的长．

【提示】

这是一个存在性命题，由于五个向量是任意、故很难从正向直接推证，可采用反证法．

【证明】

考虑五个向量，，，，，假设其中任意两个向量和的长均大于其余三个向量和之长，则有

＋＞＋＋，

∴　²＋2·＋²＞²＋²＋²＋2（·）＋2·＋2·．

这里类似上面的＋（i ≠j）．共有10种情况，这10个不等式，左边、右边分别相加，得

4（²＋²＋…＋²）＋2＞6（²＋²＋…＋²）＋6．

整理值有　＋＋＋＋²＜0．

这是不可能的，故假设不真，原命题得证．

【点评】

本题就知识而言重点考查向量的数量积运算：就方法而言考查了反证法的数学方法．就能力而言考查了思维能力及严密的推理论证能力．题目所证虽然是存在性问题，能从五个向量中，找到一种情况即可．但由于已知向量的任意性，使得情况变的复杂，逐一排除进行挑选确定难度很大，运用等价命题的思想采用反证法十分凑效．