提高测试（一）
（一）选择题（每题4分，共24分）
1．如图，在△ABC中，点D、E、F分别为BC、AC、AB的中点，以图中各点为端点的有向线段所表示的向量中，与
的向量最多有（ ）．
（A）3个 （B）4个 （C）6个 （D）7个
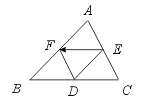
【提示】据已知，与共线的向量有
，
，
，
，
，
，
．
【答案】（D）．
【提示】本题考查共线向量的概念．注意两个共线向量的方向可以相同，也可以不同．
2．已知向量
＝（1，2），
＝（3，1），
＝（11，7）．若＝k＋l，则k、l的值为（ ）．
（A）－2，3 （B）－2，－3
（C）2，－3 （D）2，3
【提示】据已知，有（11，7）＝k（1，2）＋l（3，1），可得关于k，l的二元方程组
解之即可．
【答案】（D）．
【点评】本题主要考查平面向量的基本定理，以及向量相等的充要条件．
3．已知四边形ABCD的四个顶点坐标分别是A（1，2），B（4，0），C（8，6），D（5，8），有下面四个结论：
① 四边形ABCD是平行四边形
② 四边形ABCD是矩形
③ 四边形ABCD是菱形
④ 四边形ABCD是正方形
其中正确的结论是
（A）①② （B）①③ （C）①②④ （D）①③④
【提示】
由
＝（3，－2），＝（3，－2），即＝，得四边形ABCD是平行四边形，结论①正确；又＝（4，6），得·＝12－12＝0，即BC ⊥AB，□ABCD是矩形，结论②正确；而＝
，＝2，即≠，故结论③、④均不正确．
【答案】（A）．
【点评】
本题考查向量的坐标运算，数量积，向量垂直的充要条件，两点间的距离公式．即利用向量的有关知识，判定平面图形的几何特征．通常情况下，对于任意四边形，利用向量共线，判断是否为梯形；利用向量相等，判断是否为平行四边形．对于平行四边形，再利用数量积为零，判断是否为矩形，利用相邻两边所表示向量的模的大小．判断是否为菱形．
4．已知△ABC的三个顶点坐标分别为A（－1，－4），B（5，2），C（3，4），则角B等于（ ）．
（A）90° （B）60° （C）45° （D）30°
【提示一】可由已知顶点坐标，利用两点间距离求出三条边长，再用余弦定理求角B．
由已知，可得
AB ＝
＝6
，
BC ＝
＝2，
AC ＝
＝4
．
由余弦定理，得
cos B ＝
＝
＝0．
∴ ∠B ＝90°．
【提示二】
利用向量知识，求角B，就是求向量
与的夹角．由三个顶点的坐标，得＝（6，6），＝（－2，2）．＝6，＝2．
∴ cos B
＝
＝
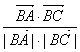＝0．
得 ∠B ＝90°．
实际上，由·＝6×（－2）＋6×2＝0，便可知⊥，于是∠B ＝90°．
【答案】（A）．
【点评】
本题考查向量知识的灵活应用，以及解斜三角形的有关知识．考查运算能力，本题运用向量垂直的充要条件，由平面向量的坐标表示．求得角B等于90°，最为简捷．
5．将函数y ＝f（x）的图象按＝（－2，3）平移后，得到的是函数y ＝
的图象，则y ＝f（x）的表达式为（ ）．
（A）y ＝＋3 （B）y ＝
＋3
（C）y ＝
－3 （D）y ＝
【提示】
利用平移公式，设P（x，y）为y ＝f（x）图象上任一点，按＝（－2，3）平移后的坐标为P′(x′，y′)，则
即
据已知，点P′满足
y′＝4 x′2－2 x′＋4，
∴ y
＋3＝
，
化简，得 y
＝－3．
【答案】（C）．
【点评】本题考查平移公式，应明确图象的平移实质上是图象上点的平移．
6．在△ABC中，若A︰B︰C ＝1︰1︰4，则a︰b︰c等于（ ）．
（A）1︰1︰2 （B）1︰1︰4
（C）1︰1︰
（D）1︰1︰16
【提示】
将边之比转化为对应角的正弦函数之比，再由正弦定理可得．
∵ 在△ABC中，A ＋B ＋C ＝180°，
由 A︰B︰C＝1︰1︰4，可得
A ＝B ＝30°，C ＝120°．
∴ sin A
＝sin B ＝
，sin C ＝
．
由正弦定理，可知
a︰b︰c ＝sin A︰sin B︰sin C ＝1︰1︰．
【答案】（C）．
【点评】
本题根据已知条件，把求边的比的问题转化为关于角的问题，考查了正弦定理的应用．
（二）填空题（每题4分，共20分）
1．化简· [（·）－（·）]的结果是______．
【提示】
· [（· ）－（·）]
＝·（·）－·（·）
＝（·）（·）－（·）（·）
＝0．
【答案】0．
【点评】本题考查平面向量数量积的运算律，注意数量积运算的结果为一个数．
2．已知A（2，3），B（－1，5），且
＝
，
＝－
，则CD中点的坐标是________．
【提示】
要求CD中点的坐标，必先求得点C、D的坐标．
∵ A（2，3），B（－1，5）．
∴ ＝（－3，2），
∴ ＝＝（－1，
）．
则点C的坐标为（1，
）．
又＝－＝（
，－）
由点D的坐标为（
，
）
代入中点坐标公式，得
（
，
），即（
，
）．
【答案】（，）．
【点评】本题考查共线向量，向量的坐标运算及线段的定比分点的坐标公式．本题也可代入线段的定比分点的坐标公式．由＝，得＝，即点C分所成的比为，可得点C的坐标；由＝－，得＝－
，即点D分所成的比为－，可得点D的坐标．
3．在△ABC中，已知B ＝135°，C ＝15°，a ＝5这个三角形的最大边长为______．
【提示】
由已知B ＝135°为三角形中的最大角，其对边b为所求的最大边．
先由已知的B ＝135°，C ＝15°，求得
A ＝180°－（B ＋C）＝30°．
再由正弦定理，得
b ＝
＝
＝5．
∴ △ABC的最大边长为5．
【答案】5．
【点评】本题主要考查应用正弦定理解决三角形的有关问题．
4．把函数y ＝2 x2＋x ＋3的图象C按＝（3，－1）平移到C′，则C′的函数解析式为______．
【提示】
利用平移公式，设P（x，y）为函数y ＝2 x2＋x ＋3图象C上的任一点，经平移后，对应点P′（x′，y′）在C′上，则
即
代入C的方程，得
y′＋1＝2 (x′－3)2＋(x′－3)＋3．
即y′＝2 x′2－13 x′＋17．
【答案】y′＝2 x2－13 x ＋17．
【点评】本题考查平移公式，注意移图是在确定的坐标系xOy内进行的，习惯上将x′，y′仍写成x，y，于是C′的函数解析式为x，y的关系式．
5．在△ABC中，B ＝30°，AB ＝2，S△ABC＝，则AC的长等于_______．
【提示】由已知，S△ABC＝AB · BC · sin B ＝×2×BC · sin 30°，得BC ＝，于是BC ＝2．
代入余弦定理，得
AC 2＝AB2＋BC2－2 AB · BC · cos B ＝4．
∴ AC ＝2．
【答案】2．
【点评】本题考查余弦定理的应用，在△ABC中，先由面积求出BC，问题转化为已知两边及一夹角．求第三边，应用余弦定理．
（三）解答题（每小题14分，共56分）
1．已知P为△ABC内一点，且3
＋4
＋5
＝
．延长AP交BC于点D，若＝，＝，用、表示向量、．
【提示】
注意到＝－，＝－，由已知3＋4＋5＝，可以得到关于、的表达式，化简即可．对于，可利用与共线予以解决．
【答案】
∵ ＝－＝－，
＝－＝－，
又 3＋4＋5＝，
∴ 3＋4（－）＋5（－）＝，
化简，得＝＋
．
设＝t（t∈R），则
＝t ＋t． ①
又设 ＝k（k∈R），
由 ＝－＝－，得
＝k（－）．
而 ＝＋＝＋，
∴ ＝＋k（－）
＝（1－k）＋k ②
由①、②，得
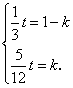解得 t ＝
．
代入①，有
＝
＋
．
【点评】
本题是以、为一组基底，寻求、关于、的线性分解式，主要考查了向量的加法．实数与向量的积及运算律，两个向量共线的充要条件，平面向量基本定理，求时，利用了以、为基底的的分解式是唯一确定的，这是求线性分解式常用的方法．
2．在△ABC中，a ＋b ＝10，而cos C是方程2 x2－3 x －2＝0的一个根，求△ABC周长的最小值．
【提示】
三角形周长为a ＋b ＋c，而a ＋b ＝10已知，故求△ABC周长的最小值．就是求C的最小值，由方程的根可解得cos C的值，借助余弦定理得c与a（或b）的关系，再确定C的最小值．
【答案】
解方程2 x2－3 x －2＝0，得
x ＝2或x ＝－．
∵ cos C≤1，
∴ cos C
＝－．
由余弦定理，得
c2＝a2＋b2－2 ab cos C
＝a2－b2＋ab
＝(a ＋b) 2－ab，
而 a ＋b ＝10，
∴ c2＝100－a（10－a）
＝a2－10 a ＋100
＝(a －5)2＋75．
∴ 当a ＝5时，c有最小值
＝5．
∴ △ABC的周长为 10＋5．
【点评】
本题综合考查余弦定理，二次函数的极值等内容．通过分析题目已知条件，将求三角形周长最小值问题转化为求c边的最小值问题．借助已知条件和余弦定理，建立了关于a的二次函数关系，利用二次函数最值的结论确定出c的最小值，使向量得解．在解决问题的过程也考查分析问题．解决问题的能力．