高一上学期期中综合检测2
【同步达纲练习】
时间(120分钟，满分150分)
一、选择题(每小题5分)
1.若全集为U＝R，A＝｛x｜x＜1
，B＝｛x｜x＞0｝，那么CU(A∪B)等于( )
A.｛0｝ B.｛0，1｝ C.(-∞，0)∪［1，+∞］ D.
2.集合A＝｛x｜x2-5x+4≤0｝，B＝｛x｜x2-5x+6≥0｝，则A∩B等于( )
A.｛x｜1≤x≤2，或3≤x≤4｝ B.｛x｜1≤x≤2，且3≤x≤4｝
C.｛1，2，3，4｝ D.｛x｜1≤x≤4或2≤x≤3｝
3.若A∪B＝U(全集)，下列关系一定正确的是( )
A.B
(CUA) B.A∩B＝ C.(CUA)B D.(CUA)∩(CUB)＝U
4.当｜x-2｜<a时，不等式｜x2-4｜<1成立，则正数a的取值范围是( )
A.a>
-2 B.0<a≤-2 C.a≥-2 D.a>
+2
5.若不等式5-x>7｜x+1｜和不等式ax2+bx-2>0的解集相同，则a、b的值分别是( )
A.a＝-8,b＝-10 B.a＝-1,b＝9 C.a＝-4,b＝-9 D.a＝-1,b＝2
6.命题p∶(x-1)·(y-2)＝0
命题q∶(x-1)2+(y-2)2＝0，命题p是命题q的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.由下列各组命题构成“p或q”、“p且q”、“非p”形式的复合命题中，p或q为真、p且q为假、非p为真的是( )
A.p∶3是偶数，q∶4是奇数 B.p∶3+2＝6，q∶5>3
C.p∶a∈(a,b),q∶｛a｝
｛a, b｝ D.p∶QR，q∶N＝Z
8.以下四个对应：
(1)A＝N+，B＝N+，f:x→｜x-3｜.
(2)A＝Z,B＝Q,f:x→
.
(3)A＝N+,B＝R,f:x→x的平方根.
(4)A＝N，B＝｛-1,1,2,-2｝,f:x→(-1)x.
能构成从A到B的映射有( )个
A.1 B.2 C.3 D.4
9.若
为实数，则函数y＝x2+3x-5的值域是( )
A.(-∞，+∞) B.［0，+∞） C.［-7，+∞） D.［-5，+∞）
10.如果f(
)＝
，则当x≠0，1时，f(x)等于( )
A. B.
C. D. 
-1
11.已知函数f(x)在区间［a,b］上单调，且f(a)·f(b)<0，则方程f(x)＝0在区间［a,b］内( )
A.至少有一实根 B.至多有一实根
C.没有实根 D.必有唯一的实根
12.已知f(x)是偶函数，它的定义域为R，在［0，+∞）上递减，那么一定有( )
A.f(-
)>f(a2-a+1) B.f(-)≥f(a2-a+1)
C.f(-)<f(a2-a+1) D.f(-)≤f(a2-a+1)
二、填空题(每小题4分)
13.已知实数a∈［-1，1］则当x∈ 时，函数f(x)＝x2+(a-4)x+4-2a的值是正的.
14.已知A和B是两个命题，如果A是B的充分条件，那么B是A的 条件，┐A是┐B的 条件.
15.若f(x)＝(m-1)x2+mx+3(x∈R)是偶函数，则f(x)的增区间是 .
16.关于反函数有下列命题：
①二次函数一定有反函数；
②反比例函数一定有反函数；
③若函数y＝f(x)与其反函数y＝f-1(x)有公共点P，则P点一定在直线y＝x上；
④奇函数一定有反函数；
⑤单调函数在其单调区间上一定有反函数；
⑥偶函数一定没有反函数.
以上命题中，正确的命题的序号是 .
三、解答题(74分)
17.(9分)解不等式｜5x+2｜<7
18.(13分)已知集合A＝｛(x,y)｜y＝-x2+mx-1,m∈R｝，B＝｛(x,y)｜y＝-x+3,0≤x≤3｝，若A∩B是单元素集合，求实数m的取值范围.
19.(12分)50名学生参加跳远和铅球两项测验，跳远和铅球两项及格的人数分别是40人和35人，两项测验均不及格的有5人，求两项测验都及格的有多少人?
20.(12分)已知f(x)是定义在R上的偶函数，其图像关于直线x＝2对称，且当x∈(-2，2)时，f(x)＝-x2+1，求x∈(-6,-2)时，f(x)的表达式.
21.(14分)有三块合金，第一块是60%铝和40%铬，第二块是10%铬和90%钛，第三块是20%铝、50%铬和30%钛.现需由它们组成一块含钛45%的新的合金，试问在新的合金中，含铬的百分比的范围?
22.(14分)设函数f(x)是定义在(-∞，+∞)上的增函数，如果不等式
f(1-ax-x2)<f(2-a)
对于任意x∈［0，1］都成立，求其中实数a的取值范围.
参考答案
【同步达纲练习】
一、1.D 2.A 3.C 4.B 5.C 6.B 7.B 8.A 9.D 10.B 11.D 12.B
二、13.｛x｜x<1或x>3｝ 14.必要 必要 15.(-∞，0］ 16.②⑤⑥
三、17.解：将不等式两边平方得
25x2+20x+4<49，即5x2+4x-9<0,
解之得，-1
<x<1.
18.解：由题意知，原命题等价于方程-x2+mx-1＝-x+3在0≤x≤3时，只有一解.
(1)对于方程-x2+mx-1＝-x+3，即x2-(m+1)x+4＝0,
当Δ＝(m+1)2-16＝0时，m＝3或m＝-5.
若m＝3，则x＝2符合题意；
若m＝-5，则x＝-2不符合题意，应舍去.
(2)对于方程x2-(m+1)x+4＝0,
当Δ＝(m+1)2-16>0时，令f(x)＝x2-(m+1)x+4.
是由f(0)·f(3)<0，得m>
.
综合(1)、(2)，满足题意的m应为m＝3，或m>.
19.解：设U＝｛参加跳远和铅球两项测验的同学｝，A＝｛跳远测验及格的同学｝，B＝｛铅球测验及格的同学｝.
如下图所示，知40+35+5-50＝30.
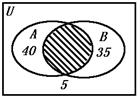
这个30，即图中的阴影部分元素的个数，也即是跳远和铅球两项都及格的人数.
20.∵-6<x<-2,∴-2<x+4<2
∴f(x+4)＝-(x+4)2+1.
又f(x)的图像关于直线x＝2对称，
∴f(-x)＝f(4+x)
由f(x)是偶函数，∴f(-x)＝f(x)
∴f(x)＝f(x+4)＝-(x+4)2+1,x∈(-6,-2).
21.0.25≤a≤0.4.
22.(-∞，1).