高一上学期数学期末考试

高一上学期数学期末考试

注：本试卷分选择题、填充题、解答题三部分，考试时间120分钟，满分150分）

（I　选择题部分，共60分）

一、选择题（本大题共12小题，每题5分，共60分，要求把正确的选择支填涂到答题卡上．）

1、设全集为R，A＝{x－4＜x＜1，B={xx≤－4}，c＝｛xx≥｝则C是A与B的

  A、交集　B、并集　C、交集的补集　 D、并集的补集

2、满足{a}的集合M共有

  A、6个　B、7个　C、8个　D、9个

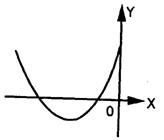
3、函数f（x）=ax²+4x+（a—3）的图象如图所示，

  则a的取值范围是：

  A、a＜0  B、a＞3　C、4＞a＞3　D、－l＜a＜3　　　　　  MMX

4、式子的值为

　A、30　　B、25　 C、10　 D、2

5、若x＞与＜2同时成立，则x的范围为

　A、（－，）　　  B、（－∞，－）∪（，+∞）

C、（，+∞）　　　 D、（－∞，－）∪(，+∞)

6、等差数列{a_n}中a₁＞0，S₄=S₅，则该数列前多少项的和取得最大值

  A、5　B、6　 C、7　 D、8

7、已知全集U，集合P，Q，下列命题：P∩Q＝P，P∪Q＝Q，P∩(_UQ)=Q，（_UP）∪Q＝U，其中与命题PQ等价的有

  A、1个　 B、2个　 C、3个　 D、4个

8、集合M＝{xx＞2}，P＝｛xx＜3，那么“x∈M或x∈P”是“x∈M∩P”的

A、充分非必要条件B、必要非充分条件　C、充要条件D、即不充分又不必要条件

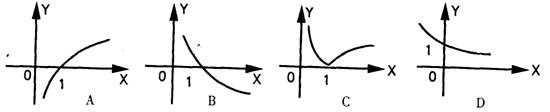
9、函数f（x）＝－log_a（0＜a＜l＝的图象大致是

10、已知项数相同的两等比数列{a_n}{b_n}与之相关的下列五个数列①{a_n+b_n}②{a_n－b_n}③{c·a_n·b_n}④{a_n+c }c≠0 ⑤，其中一定是等比数列的是{b_n}{a_n}{b_n}

　　 A、①②⑤　 B、③⑤　　 C、②③④　  D、④⑤

11、已知函数y=f(x)定义在〔－2，l〕上，且f（－l）＞f（0），则下列判断正确的是

  A、f（x）在[－2，l]上必定是增函数　 B、f（x）在[－2，l]上必定是减函数

  C、f（x）在[－2，l]上不是增函数　　 D、f（x）在[－2，l]上不是减函数

12、已知函数y＝f（x）的反函数与 y＝g（x）的图象关于点 P（a，b）对称，则g（x）=

  A、a+f^－1（b+x） B、2a－f^－1（2b－x）　C、b+f^－1（a＋x）　D、2b－f^－1（2a－x）　　　　　　　  二、填充题（本大题共4小题，每题4分．共16分，要求直接填写在相应的横线上．）

13、已知f（2^－x－2）＝4^x+2，则f(0)=　　　　　　  ．

14、x+2＞x－1的解集为：　　　　  ．

15、已知定义在 R上的偶函数 y= f（x）在[0，+∞]上为减函数，且f（－）=0，则f[]＜0的x的范围为：　　　　　　　　 

16、一道题目，一个同学会做，后在八分钟内教会另两个，而且他只教两个同学．这两上同学又在八分钟内各教会其他不会做的两个同学，如此下去，全班54名同学，人人会做共需时间　　　　　　  （分钟）．

三、解答题《本题有6小题，共74分，要求写出推理或运算过程。》

17、（本题12分）

已知A={xx－a＜4，B＝{xx－2≥3}

（l）若A∪B=R，求a的范围；

（2）若AB，求a的范围．

18、（本题12分）

设原命题“若 a²+2ab+b²+a+b－2≠0，则a+b≠1”

（1）写出该命题的逆否命题；

（2）请证明原命题为真．

19、（本题12分）

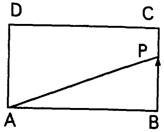
如图在矩形ABCD中，AB=4，BC＝3，动点P

以每秒1的速度从点B出发，沿折线BCDA移

动到A为止，设动点P移动的时间为t，⊿ABP

的面积为y，

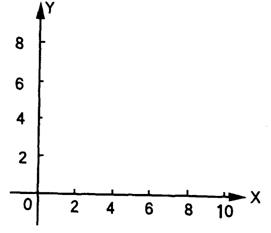
求y关于时间t的函数解析式，并作图．

20、（本题12分）

某建房公司以100万元买了一块地，计划造一幢每层为1000平方米的楼房n层，第一层每平方米的造价为600元（不含买地费用），第M层为700元，每升高一层每平方米的造价增加100元．在计算每平方米平均造价时要把买地费用计人．

(1)写出整个大楼每平方米的平均造价y关于n的解析式；

(2)为使每平方米平均造价不超过1150元，这楼最多造几层？

21、（本题12分）

已知函数f(x)=(x∈R)

（1）求反函数y＝f^－1（x）；

（2）判断y=f^－1（x）的奇偶性（写出判断过程）；

（3）证明函数y=f^－1（x）在R上是增函数．

22、（本题 14分）

已知数列｛a_n｝，其中a₁=l，a_n＝a_n－1·2^n－1（n≥2，n∈N*）

（1）求a₂ ，a₃的值；

（2）求通项a_n ；

（3）设S_n=log₂()，数列｛b_n｝的前n项和为S_n，求数列｛b_n｝的前n项的和_n

答案

一、

1、D　 2、B　　3、C　　 4、A　　5、D　　6、D　　7、D　

8、B　 9、B　　10、B　　11、C　 12、D

二、

13、2　 　14、{xx＞－}  15、(0，) ，(3，+∞) 　　16、40

三、

17、①1≤a≤3　　②

18、解：（1）逆否命题是“若a+b=1，则a²+2ab+b²+a+b－2=0”

（2）证明逆否命题为真．

∵a+b－1=0，∴（a+b－1）（a+b+2）=0即a²+2ab+b²+a+b－2=0，

由命题的等价性可知原命题为真

19、解：　　 2t　　　 0≤t≤3

（1） y=　　 6　　　 3＜t≤7

20－2t　　7＜t≤10

（2）　　　　　  y

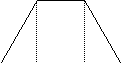
0　　　　　　　　　　  x

20、解：（Ⅰ）y=100[]

（Ⅱ）≤11.5　　n∈N*

∴n=2或n=10　　∴最多可造10层。

21、解：（Ⅰ）f^－1(x)=　x∈R

（Ⅱ）y=f^－1(x) 为奇函数（证略）

 （Ⅲ）（证略）

22、解：

（1）a₂ =2，a₃=8；

（2）a_n =；

（3）b_n=n－4，b_n=

　　　　 　 (n≤4)

S_n =

　(n＞4).