高一数学（下）第四章三角函数检测题
班级____ 姓名________ 得分_____
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，
满分150分。考试时间120分钟。
第I卷（选择题60分）
一、 选择题(本大题共有12小题, 每小题5分, 共60分)
1.若
的周期是
的奇函数,则
可以是 ( )
A.
B.
C.
D.
2.函数
在区间[a,b]上是增函数,且
,
,则
在[a,b]上（ ）
A.是增函数 B.是减函数
C.可以取得最大值M D.可以取得最小值
3.函数
的最大值是 ( )
A.
B. 
C. 
D. 
4.已知
,那么下列命题成立的是 ( )
A.
若
、
是第一象限角,则
B.
若、是第二象限角,则
C.
若、是第三象限角,则
D.
若、是第四象限角,则
5.函数
的最小正周期是 ( )
A.
B. C.
D.
6.设、是一个钝角三角形的两个锐角,下列四个不等式中
不正确的是 ( )
A.
B.
C.
D.
7.若
,且
,则是 ( )
A.第一、二象限角 B.第一、三象限角
C.第一、四象限角 D.第二、三象限角
8.已知
, 
, 
等于 ( )
A.
B.
C.
D.1
9.等式
成立的充要条件是 ( )
A.
中至少有一个为
B.
C.
中至少有一个为
D.
10.已知是第三象限角,且
, 则
( )
A. B.
C.
D.
11.在直角三角形中, 两锐角为A和B, 则
( )
A.
有最大值
和最小值0
B.
有最大值,但无最小值
C. 既无最大值也无最小值
D.
有最大值2和最小值
12.如果函数
的图像关于直线
对称,
那么
( )
A.
B.
C.1 D.
第II卷（非选择题90分）
二.填空题(本大题共有4小题,每小题4分,共16分)
13.已知
,
,则
的值是________.
14函数
的定义域是________.
15.若函数
的最小值为1, 则_______.
16.给出下列命题：
①
存在实数，使
;
②函数
是周期为的偶函数;
③若、是第一象限角，且
，则;
④若
，则
.
其中正确的命题的是__________(注:把你认为正确的命题的
序号都填上).
三.解答题(本大题共有6小题,共74分)
17.（10分）已知
，求
的值.
18.（10分）若
.
求: 
的值.
19.（12分）已知函数
的
定义域是
,值域是[
,求常数
的值.
20.（14分）已知函数
（1）
求的定义域和值域
（2）
判断的奇偶性和周期性
（3）
求的单调区间
21.（14分）若
恒成立，
求实数m的取值范围.
22.（14分）已知
证明: 
高一数学（下）第四章三角函数检测题参考答案
一、选择题(本大题共有12小题,每小题5分,共60分)
BCBDB DCACD BD
二、填空题(本大题共有4小题,每小题4分,共16分)
13. 14.
15. 17.5 16.②④
三、解答题(本大题共有6小题,共74分)
17.(满分10分)
由
, 有
, 4分
即
,于是
,
又
,故
,
8分
所以
10分
18.（满分10分）
设方程的两根为
,
程有两个不相等的正根,
⊿=
(1)
又
,
(2)
(3)
6分
由(1)得
,
由(2)得
,
由(3)得
，
9分
于是 
，
又因为
为锐角, 所以
10分
19.（满分12分）
4分
由
得
,
此时,
6分
当>0时,y的最大值是2+
,最小值是 -+
依题意
当<0时,y的最大值是-+,最小值2+
依题意
10分
20.（满分14分）
(1)定义域为
值域为
5分
(2)由于函数的定义域在数轴上关于原点不对称，
所以函数是非奇非偶函数,
是周期函数，周期为.
10分
(3)函数的单调减区间为
,
单调增区间为
.
14分
21.（满分14分）
由
得
，
设
，则
[
，1]上式化为
（1）
由题意，（1）式在[，1]上恒成立.
4分
记
，这是一条开口向上抛物线，
再记
，
则有
，
（2）
6分
或
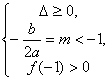（3）
8分
或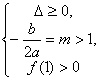
（4）
10分
解（2）（3）（4）得
14分
22.（满分14分）
，
6分
其中
,
所以
,
从而有
, 10分
由此得
.
,
即.
11分