高一数学测试题—等差数列
一、选择题：
1、有下列五个命题：
①数列{a n}成等差数列的充要条件是对任意的n∈N*,a n+1－a n 是非零的常数；
②首项为a,公差为d的等差数列用递推式表示,就是a 1=a, a n+1 = a n +d( n=1,2,3…)
③等差数列{a n}的通项公式a n必是关于n的一次函数
④b是a,c的等差中项的充要条件是2b=a+c
⑤若等差数列{a n}的公差不为零,则对任意的m、n、p、q∈N*,总有a m+a n = a p+a q
m + n = p + q.
其中正确命题的个数为 （ ）
A．1 B．2 C．3 D．4
2、若a≠b,数列a,x1,x
2 ,b和数列a,y1
,y2 ,b都是等差数列，则 
（ ）
A．
B．
C．1
D．
3、等差数列{a n}的前三项为x－1, x+1, 2x+3,则这个数列的通项公式为 （ ）
A．a n =2n－5 B．a n = 2n－3
C．a n =2n－1 D．a n =2n+1
4、在等差数列{a n }中，S 4 =1, S 8 =4,则a 17 +a 18 +a 19+a 20 的值是 （ ）
A．7 B．8 C．9 D．10
5、已知等差数列的首项为31,若此数列从第16项开始小于1，则此数列的公差d 的取值范围是 （ ）
A．(－∞,－2) B．[－
, －2] C．(－2, +∞) D．(— ,－2)
6、已知无穷等差数列{a n}，前n项和S n 中，S 6 <S 7 ,且S 7 >S 8 ,则 （ ）
A．在数列{a n }中a7 最大； B．在数列{a n }中,a 3 或a 4 最大；
C．前三项之和S 3 必与前11项之和S 11 相等； D．当n≥8时，a n <0.
7、一群羊中,每只羊的重量数均为整数公斤数,其总重量为65公斤,已知最轻的一 只羊重7公斤,除去一只10公斤的羊外,其余各只羊的公斤数恰好能组成一个等 差数列,则这群羊共有 （ ）
A． 6只 B．5只 C．8 只 D．7 只
8、等差数列{a n}中,当m≠2001时,有a 2001 =m , a m = 2001,若p∈N*且p>a m,则a m+p与0
的大小关系是 （ ）
A．a m+p >0 B．a m+p = 0 C．a m+p <0 D．无法确定
二、填空题：
9、等差数列{a n }中,a 2n ∶a n = (4n－1)∶(2n－1),则S2n ∶S n = ________.
10、已知集合M={mm=7n,m∈N*,m<100},则M中元素的个数为_____,所有元 素的和为______.
11、在等差数列{a n }中,已知a 1+a 2 +……+a 10 = p, a n－9 +a n－8 +……+a n = q,则其前ｎ项的和S n =______.
12、两个等差数列，它们的前ｎ项的和之比为
,则该数列的第9项之比为_
_____
.
三、解答题：
13、己知{a n }为等差数列,a 1=2,a2 =3,若在每相邻两项之间插入三个数，使它和原数列的数构成一个新的等差数列，求：
①原数列的第12项是新数列的第几项？
②新数列的第29项是原数列的第几项？
14、已知等差数列{a n }的公差是正数,且a 3 ·a7 =－12, a4 +a 6 =－4,求它的前20项的和S 20 .
15、设等差数列{a n }的前ｎ项的和为S n ,且S 4 =－62, S 6 =－75,求：
①{a n }的通项公式a n 及前ｎ项的和S n ；.
②a 1 +a 2 +a 3 +……+a 14 .
16、已知数列{a n },首项a 1 =3且2a n+1=S n ·S n－1 (n≥2).
①求证：{
}是等差数列,并求公差；
②求{a n }的通项公式；
③数列{an }中是否存在自然数k0,使得当自然数k≥k 0时使不等式a k >a k+1 对任意大于等于k的自然数都成立,若存在求出最小的k值,否则请说明理由.
高一数学测试题—参考答案
等差数列
一、CBBCB DAC
二、（9）7 （10）14,735 （11）
（12）
三、（13）分析：应找到原数列的第n项是新数列的第几项，即找出新、旧数列的对应关系.
解：设新数列为
即3=2+4d，
即原数列的第n项为新数列的第4n－3项.①当n=12时，4n－3=4×12－3=45，故原数列的第12项为新数列的第45项.②由4n－3=29,得n=8，故新数列的第29项是原数列的第8项.
注：一般地，在公差为d的等差数列每相邻两项之间插入m个数,构成一个新的等差数列，则新数列的公差为
原数列的第n项是新数列的第n+(n－1)m=(m+1)n－m项.
（14）分析：可直接用通项公式代入求得a1和d，再代入S20公式.也可以利用等差数列的性质，运用方程的思想来求解.
|
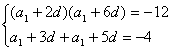
由②，有a1=－2－4d,代入①，有d2=4,再由d>0，得d=2.
（法二）：由等差数列的性质可得：a4+a6=a3+a7即：a3+a7=－4，又a3·a7=－12,由韦达定理知：
a3，a7是方程x2+4x－12=0的两根.解方程可得，x1=－6,x2=2
注：这是等差数列中运用方程的思想的典型问题，应注意首项a1和公差d的特殊作用.（15）分析：通过解方程组易求得首项和公差，再求an及Sn；解答②的关键在于判断项的变化趋势。
解：设等差数列首项为a1，公差为d，依题意得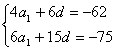
解得：a1=－20,d=3. ①
②
|
（16）分析：证
为等差，即证
（d是常数）解：①由已知当
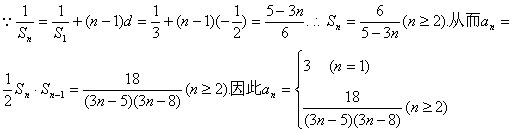
③