高一数学测试题—定比分点及平移（8）
一、选择题：
1、将点(2,－5)按向量a=(－3,4)平移后得对应点的坐标为 （ ）
A．(－1,－1) B．(5,－9) C．(－1,－9) D．(5,－1)
2、点P(2,－1)平移后变成了P'(－2,1),则坐标原点平移后对应点的坐标是 （ ）
A．(4,2) B．(4,－2) C．(－4,2) D．(－4,－2)
3、函数f(x)=
的反函数f －1(x)的图象的对称中心是(－1,3),则实数a等于 （ ）
A．2 B．3 C．－2 D．－4
4、将函数y=f(x)图象上的点P(1,0)平移变为P'(2,0),平移后得到新图象的函数解 析式为 （ ）
A．y'=f(x'－1) B．y'= f(x')－1 C．y'=f(x'+1) D．y'=f(x')+1
5、函数y=sin2x的图象按向量a平移后，所得函数的解析式是y=cos2x+1,则a等于（ ）
A．(
,1)
B．(－ ,1) C．(－
,1) D．(,1)
6、已知函数y=3(x－1)2的图象为C1,y=3(x+1)2的图象为C2,那C2的图象是由C1的图象( )得到的.
A．向左平移1个单位 B．向右平移1个单位
C．向左平移2个单位 D．向右平移2个单位
7、设点P分
所成的比为λ,P在AB的延长线上,则 （ ）
A．λ<－1 B．－1<λ<0 C．0<λ<1 D．λ>1
8、点A(2,0),B(4,2),若AB=2AC, 则C点的坐标为 （ ）
A．(－1,1) B．(－1,1)或(5,－1) C．(－1,1)或(1,3) D．无数多个
二、填空题：
9、已知点A(4,2)、B(－6,－4)、C(x,－2
)三点共线,则C点分AB的比λ=____,
x=_____.
10、已知平行四边形三个顶点坐标分别为(－1,0)、(3,0)、(1,－5),则第四个顶点 坐标为__________________________.
11、已知点P(2,－3),按向量a= (t2+3t－12,t2+2t－5)平移得到P'(0,0),则t=____.
12、把函数y=log3(x+3)－6的图象,按向量a平移,得到函数y=log3x的图象,则a= ______.
三、解答题：
13、已知三角形的三个顶点是A(4,1),B((7,5),C(－4,7),求ΔABC的∠A的平分线 AD的长.
14、①把点A(3,5)按向量a =(4,5)平移,求平移后对应点A'的坐标.
②把函数y=2x2的图象F按向量a = (2,－2)平移到F',求F'的函数解析式.
15、将抛物线y=x2－4x+5 按向量a平移,使顶点与原点重合，求向量a的坐标.
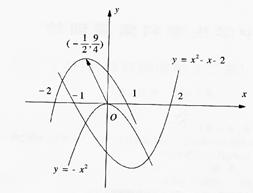
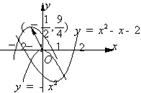
16、将函数y=－x2进行平移，使得到的图形与函数y=x2－x－2的图象的两个交 点关于原点对称.(如图)求平移向量a及平移后的函数解析式.
|
高一数学测试题—参考答案
定比分点及平移
一、ACAAB CAD
二、（9）4、－4 （10）（1，5）或（－3，－5）或（5，－5）. （11）2 （12）（3，6）
三、（13）分析：要求AD的长，关键在于求出D点坐标，而由平面几何中三角形内角平分线性质定理有AC∶AB=CD∶DB可求出D点分CB所成的比，再由定比分点公式即可求出D点坐标
解：
0
又
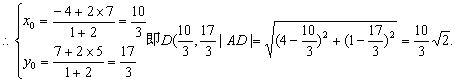注：在本例中还可以求出∠A的外角平分线与CB延长线的交点坐标等.（14）解：①设
，根据平移公式得：
②设P（x，y）为F上的任一点，它在
上的对应点为
，由平移公式得：
将它代入到y=2x2中，得到
，即
即的函数解析式为
.
注：求此类平移后对应点的坐标或对应图形的函数解析式，关键在于确定平移公式.（15）解法一：（配方法）由
得
，于是顶点为（2，1）按向量a将它平移的对应点是（0，0），因此
解法二：（待定系数法）设a=（h，k），则有平移公式：
得：
|
即：
要使平移后的图象的顶点与原点重合当且仅当：
.注：待定系数法是平移向量的一种重要的方法，请同学们掌握. 由于运算较繁，所以我们另辟蹊径. 于是了以上的两种解法.解法一也是一种常用的方法. 配方的目的是求抛物线的顶点. 寻求平移向量目前我们有三种方法：（1）配方法（2）待定系数法（3）特征值法.（16）解法一：设平移公式为
代入
，得到
，把它与
联立，得
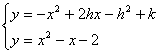设图形的交点为（x1，y1），
（x2，y2），由已知它们关于原点对称，即有：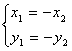
由方程组消去y得：
. 由
又将（
），
分别代入①②两式并相加，得：
. 解得
.
平移公式为：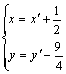
代入得：
.
解法二：由题意和平移后的图形与交点关于原点对称，可知该图形上所有点都可以找到关于原点的对称点在另一图形上，因此只要找到特征点即可.
的顶点为
，它关于原点的对称点为（
），即是新图形的顶点.由于新图形由平移得到，所以平移向量为
以下同解法一.
注：本例的解法二就是（15）所说的特征值法，此法甚妙，但要慎重.