高一数学测试题—段考试卷

高一数学测试题—段考试卷

一、　选择题：(本大题共12小题,每小题5分, 共60分)

1．若i= (1,0), j =(0,1)则与2i+3j垂直的向量是　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　　)

A．3i+2j　　　　 　B．－2i+3j　　　 C．－3i+2j　　　 　　D．2i－3j　

2．m,n∈R, 都是非零向量,且m,有公共的起点, 若终点共线, 则m,n满足　　　 (　　 )

A．m+n=1　　　　 B．m－n=1　　　 C． m + n =－1　　　D． m² + n² =1

3．已知A(1,2) 、B(5,4) 、C(x,3) 、D(－3,y) 且∥,则x、y的值分别为　　(　　 )

A．－7,－5　　　 　B． －7,5　　　　 C． 7,－5　　　　　　D． 7,5

4．在△ABC中,AB=2,AC=4, ∠A=,D为BC边中点, 则AD长等于　　　　　　　　　 (　　 )

A．1　　　　　  　 B．2　　　　　  　C．　　　　　　　 D．

5．向量与向量　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．一定平行但不相等　　　　　　　　　B．一定垂直

C．一定平行且相等　　　　　　　　 D．无法判定

6．己知的夹角为,则以为邻边的平行四边形的对角线长为　　　 (　　 )

A．15　　　　 　　　B．　　　　 C．14　　　　 　　　　D．16

7． 将函数y=f(x) 的图象按向量=(2,－1) 平移得到y = 的图象, 则f(x) 的表达式为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　 )

A．y = 3^－(x+2) +1　　　　　　　　　  B．y = 　　 

C．y = 　　　　　　　　　　 D． y=

8． 己知P₁(2,－1) 、P₂(0,5) 且点P在P₁P₂的延长线上,, 则P点坐标为(　　)

A．(－2,11)　　　　 B．(　　　　 C．(,3)　　　　　　D．(2,－7)

9．已知A(0,3) 、B(2,0) 、C(－1,3) 与方向相反的单位向量是　　　　　　 (　　 )

A．(0,1)　　　　 　 B．(0,－1)　　　 　C． (－1,1)　 　　　D．(1,－1)

10．在△ABC中,sinA：sinB：sinC = m：(m+1) ：2m, 则m的取值范围是　　　　　　　(　　 )

A．m >－　　  　B．m<0　　　　　　C．m>　　　　　　 D．m>2

11．已知：且∥,⊥,则点C的坐标为　　 (　　)

A．(－3,－)　　　　　　　　　　　　　　　　　B．(－3,)　　 　　C． (3, )　　　　D．(3,－)

12．在△ABC中, 已知C=2B, 则等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　)

A．　　　　　 　B．　　　　　 C．　　　　　 　　D．

二、　填空题：(本大题共4个小题, 每小题6分, 共24分)

13．己知,把向量绕点A逆时针旋转,得到向量,则向量

14．,则的夹角为_______.

15．在△ABC中, 若cosA=,sinB=,则cosC=_________.

16．已知若∥且方向相反, 则的坐标是________.

三、解答题：(本大题共6个小题, 共66分)

17．(本题10分)已知

①　　 求；　

②当k为何实数时,k与平行, 平行时它们是同向还是反向？

18．( 本题10分)已知与的夹角为,若向量与垂直, 求k.

19．( 本题12分)如果△ABC的三边a、b、c满足b² + c ² = 5a²,BE、CF分别为AC边与AB上的中线, 求证：BE⊥CF.

20．( 本题12分)甲船在A处遇险,在甲船正西南10海里B处的乙船收到甲船的报警后,测得甲船是沿着方位角105°的方向,以每小时9海里的速度向某岛靠近,如果乙船要在40分钟内追上甲船,则乙船应以多少速度、沿什么方向航行？

21．( 本题12分)ΔABC中，若已知三边为连续正整数,最大角是钝角.

①求最大角；

②求以它的最大角为内角,夹此角的两边之和为4的平行四边形的最大面积.

22．(本题12分)已知三角形的三个顶点是A(4,1),B((7,5),C(－4,7),求ΔABC的∠A的平分线AD的长.

高一数学测试题—期中试卷

三、  ABDB　　 AAAAC　　BD　

四、  13． ( －2,1)　　14．　 15． －　　 16． (－,－2)

五、  17．①= (1,0) + 3(2,1) = ( 7,3) , ∴= =.

②k= k(1,0)－(2,1)=(k－2,－1). 设k=λ(),即(k－2,－1)= λ(7,3),

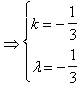∴  . 故k= 时, 它们反向平行.

18．=2×1×=1.　　∵与垂直,

∴()= , ∴2  k = － 5.

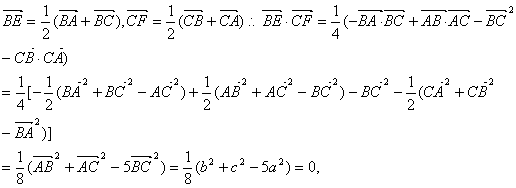 ∴⊥, 即 BE⊥CF .

20． 以21海里/小时, 沿东偏北47’ 航行.

21． 解：①设a= n－1,b= n, c= n+1,n∈N,且n>1.　　∵C为钝角,

∴ cosC =　 =  <0.　 ∵1<n<4 , n∈N,　 ∴ n= 2 或3.

当n=2时, a=1,b=2,c=3,不能构成三角形.　当n= 3时,a= 2,b= 3,c= 4.　 cosC=－ ,

 由查表或计算器得最大角C=109°29'.　 ②设夹角C的两边为x,y,则x+y=4,

则平行四边形的面积S= xysinC=x(4－x)×,　∴ 当x = 2时, S max = .

注：余弦定理可以判断三角形中的角是锐角,钝角或直角. cosA>0,则∠A为锐角,cosA<0,则∠A为钝角,cosA=0,则∠A为直角.

22． 分析：要求AD的长,关键在于求出D点坐标,而由平面几何中三角形内角平分线性质定理有AC:AB=CD:DB可求出D点分CB所成的比,再由定比分点公式即可求出D点坐标.

解：∵=, =　　 

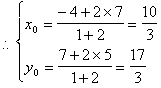又λ= === 2. 　 即D(,)

因此 = 　　　　　　　　　　　　　　　　　　　　

注：在本例中还可以求出∠A的外角平分线与CB延长线的交点坐标等.