高一第二学期数学期末复习试卷（四）
时量：100分钟 满分：100分 班级： 姓名：
一、 选择题：（每小题3分）
1．下列命题中正确的是…………………………………………………………………（ ）
（A）小于90°的角是锐角 （B）第一象限角是锐角
（C）钝角是第二象限角 （D）终边相同的角一定相等
2．已知a =（－2 , 4），b =（1 , 2）, 则a·b等于……………………………………（ ）
（A）0 （B）10 （C）6 （D）－10
3．设
，
，那么下列的点在角
的终边上的是………………（ ）
（A）（－3 , 4） （B）（－4 , 3） （C）（4 , －3） （D）（3 , －4）
4．已知
=（4 ，－2）,
=（4 ，－2），则
等于………………………（ ）
（A）（0 , 2） （B）（0 ,－2） （C）（4 , 0） （D）（0 , 4）
5．若是第一象限角，则
的值与1的大小关系是……………………（ ）
（A）
（B）
（C）
（D）不能确定
6．若a =（1 ，2），b =（－3 ，2），且（ka + b）∥（a － 3b），则实数k的值是（ ）
（A）
（B）
（C）
（D）
7．在△ABC中
，
，则
=………………………………（ ）
（A）
（B）
（C）
（D）
8．已知
，
，
，点
在线段
的延长线上，则点的坐标是………………………………………………………………………………………（ ）
（A）（－12 ，19） （B）（12 ，19） （C）（－6 ，11） （D）（0 ，
）
9．函数
和函数
在
内都是……………………………（ ）
（A）周期函数 （B）增函数 （C）奇函数 （D）减函数
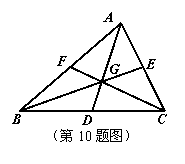10．如图, △ABC中，AD、BE、CF分别是BC、CA、AB上的中线，
它们交于点G，则下列各等式中不正确的是……………（ ）
（A）
（B）
（C）
（D）
11．已知
约等于
，那么
约等于……………………………………（ ）
（A）
（B）
（C）
（D）
12．设
，已知两个向量
，
，则向量
长度的最大值是……………………………………………………………（ ）
（A）
（B）
（C）
（D）
二、 填空题：（每小题4分）
13．将函数
的图象按向量a =（－1 ，1）平移后所得图象的解析式是______________
14．已知
，且
，则x =________________
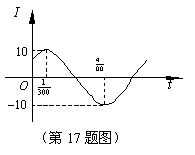15．电流强度I（安培）随时间t（秒）变化的函数I = Asin（wx+j）的图象如图所示，则当t = 
（秒）时的电流强度为_______________________
16．给出下列六种图象变换方法：
（1）图象上所有点的纵坐标不变，横坐标缩短到原来的
；
（2）图象上所有点的纵坐标不变，横坐标伸长到原来的2倍；
（3）图象向右平移
个单位； （4）图象向左平移个单位；
（5）图象向右平移
个单位；（6）图象向左平移个单位；
请用上述变换中的两种变换，将函数
的图象变换得到函数
的图象，那么这两种变换正确的标号是_______________（要求按变换先后顺序填上一组你认为正确的标号即可）
三、 解答题：（共48分）
17．（本题5分）已知
，求
的值。
18．（本题6分）已知a = 3，b =2，a与b的夹角为60°，c = 3a + 5b，d = ma－b，c⊥d，求m的值。
19．（本题7分）若
是关于x的方程
的两个实根，
（Ⅰ）求m的取值范围；
（Ⅱ）求
的取值范围。
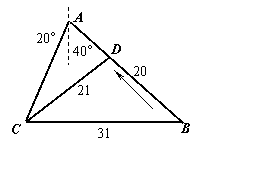20．（本题8分）某观测站C在A城的南20°西的方向，有A城出发有一条公路，走向是南40°东，由C处测得距C为31千米的公路上B处，有一人正沿公路向A城走去，走了20千米后到达D处，此时CD的间距为21千米，问这个人还走多少千米到达A城。
21．在直角坐标系中，△ABC的顶点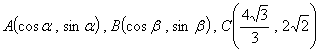
，且△ABC的重心G的坐标为
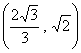，求
的值。（本题10分）
22．（本题12分）研究函数
的性质：
（Ⅰ）求函数f（x）的定义域和值域；
（Ⅱ）用定义判断f（x）的奇偶性；
（Ⅲ）在
内，作出f（x）的图象；
（Ⅳ）指出f（x）的最小正周期及单调区间。