高一第二学期数学期末复习试卷（五）
时量：100分钟 满分：120分 班级： 姓名：
一、选择题(4’×12=48’)
1、 设A=｛x︱
｝B =｛x︱︱x-1︱≥1｝则A∩B等于（ ）
A ｛x︱-1<x<5｝ B ｛x︱x≤0或 x≥2｝
C ｛x︱-1<x≤0｝ D ｛x︱-1<x≤0或 2≤x<5｝
2、 已知在
上递增函数f(x)满足f(x)=f(4-x)
x∈R，设f(
)=a f(
)=b f(4)=c则有（ ）
A a<b<c B b<a<c C c<a<b D c<b<a
3、 已知f(x-1)=x2-2x+3(x≤0)则f﹣1(x)的表达式 （ ）
A 
B 1-
C - D 
-2
4、 下列四个命题： ①若b2=ac则a,b,c成等比数列
② ｛an｝为等差数列，且常数c>0则数列｛
｝为等比数列
③ 若｛an｝为等比数列，则数列｛︱an︱｝为等比数列
④ 常数列既是等差数列又是等比数列
其中真命题的个数为（ ）
A 1个 B 2个 C 3个 D 4个
5、等差数列｛an｝中的公差d≠0,若a1,a2
,a3成等比数列，则
的值等于（
）
A 
B 
C 
D
6、要得到函数y=sin(2x-
)的图象，只需要将y=sin2x的图象 （ ）
A 向右平移
个单位 B向左平移个单位
C向右平移个单位
D向左平移个单位
7、y=
sin(-2x)-cos2x的最小值是（ ）
A - -1 B -1 C -
D 0
8、在下列各区间上，函数y=sin(x+
)的单调递增区间是（ ）
A [
,π] B [0
, ] C [ -π , 0] D [ , ]
9、函数y=
的定义域 （ ）
A ｛x︱0<x≤4｝
B ｛x︱2kπ<x≤2kπ+ ,k∈Z｝
C ｛x︱kπ<x≤kπ+ ,k∈Z｝ D｛x︱kπ-<x≤kπ+ ,k∈Z｝
10、若sinx=
(π<x<
) 则x的值等于（ ）
A 
B π
C 2π
D
11、已知tanα ,tanβ是方程x2+3x+4=0的两个根，且
<α< <β< 则 α+β = （ ）
A B 
C 或 D 
或 
12、已知P1 （6，-3）P2（-3，8）︱
︱=2︱
︱ 点P 在线段P1P2的延长线上，则P点的坐标为（ ）
A
(-12,19)
B (12,19) C
(-6,11) D (0, 
)
二、填空题（4’×4=16’）
13、设
是两个非零向量，则(+)2=()2+()2是⊥的_____________条件.
14、数列｛an｝的通项公式an=
，若sn=9则n等于_______
15、已知f(x)=ax+bsinx+1,若f(5)=7则f(-5)=__________
16、已知+=2
-8
,-= -8+16 其中︱︱=︱︱=1,⊥则·=_________.
三、解答题（10’＋8’＋8’＋8’＋10’＋12’＝56’）
17、⑴已知sin(α+β)=
,sin(α-β)=
求
⑵sinα+sinβ=
,cosα+cosβ=
求cos(α+β),cos(α-β)
18、奇函数f(x)在其定义域(
,
)上是减函数，且f(1-sinα)+f(1-sinα2)<0求角α的取值范围。
19、已知y=ax2+bx+c图象按
=(－2，4)平移到F′,已知点A（0，8）在 F′上，F与F′的交点是B（，
）试求F对应的函数的解析式。
20、在△ABC中已知（a+b+c）（a+b－c）=3ab，且cosAsinB=sinC,试判断△ABC的形状.
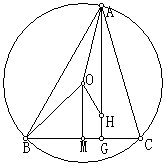21、已知锐角△ABC的外接圆的圆心为O，M为BC边上的中点，由顶点A作AG⊥BC并在AG上取一点H，使
=2
又H,M在直线BC的同一侧，且
=,
=,
=
。
⑴用、、表示与
。
⑵证明BH⊥AC,CH⊥AB。
22、若函数f(x)=asin(x－)＋b满足f()＋f()=7且f(π)－f(0)=2求:
⑴f(x)的解析式；⑵ f(x)的单调区间； ⑶ f(x)的最小值；⑷ 使f(x)=4的x的集合；