高一第二学期数学期末复习试卷（一）
时量：100分钟 满分：100分 班级： 姓名：
一、选择题（3’×12=36’）
1．tanx＞0是x＞0的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
2．函数y=cos2x－3cosx+2的最小值为 （ ）
A．2 B．0 C．－1/4 D．6
3．下列命题中正确的是 （ ）
（A）若
，则
（B）若
，则
（C），则
（D）
，则
4．点A分
所成的比为2，下列结论正确的是 （ ）
（A）A分
的比为2 （B）B分
的比为
（C）C分
的比为
（D）C分
的比为3
5．先将函数y=5sin（
－3x）的周期扩大为原来的2倍，再将新函数的图象向右平移
，
则所得图象的解析式为 （ ）
A．y=5sin（
－
） B．y=5cos
C．y=5sin（
） D．y=5sin（－2x）
6．已知
=3，
=1，且与同向，则.的值是
（ ）
A．-3 B. 0 C. 3 D. –3或3
7．已知
为锐角，且cos
=
,cos
=
，则
的值是
( )
A.
B. 
C.
或 D.或
8．下列向量中，能作为表示它们所在平面的内所有向量基底的是 ( )
A. 
B. 
C.
D.
9.平面内有
，且
，则
P1P2P3是 ( )
A.钝角三角形 B.直角三角形 C.等腰三角形 D.等边三角形
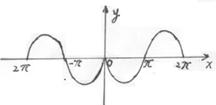10.下图中曲线对应的函数是 （ ）
（A）
（B）
（C）
（D）
11.在ABC中，B=450，c=
,b=
，则A等于
( )
A.600 B.750 C.150或750 D.750或1050
12.在ABC中，若cotA,cotB,cotC成等差数列，那么
（ ）
A. a,b,c成等差数列 B. a,b,c成等比数列 C.a2,b2,c2成等比数列 D. a2,b2,c2成等差数列
二、填空题(4’×4=16’)
13．函数y=log2x的图象按平移可得函数y=log2(x-2)+3，则=
14．函数y=sin(
)的单调递增区间是
15．设f(x)是定义域为R，最小正周期为
的函数，已知
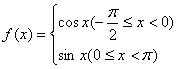则
=
.
16．关于x的函数f(x)=sin(x+
)有以下的命题：
①对于任意的，f(x)都是非奇非偶函数 ②不存在，使f(x)既是奇函数又是偶函数
③存在使f(x)是奇函数 ④对于任意的，f(x)都不是偶函数；
其中一个假命题的序号是 ,因为当＝ 时，该命题结论不正确。
三、解答题（8’+10’×4=48’）
17．已知向量
如图，请作出如下向量：（1）
（2）
18．已知0<x<, sin(－x)=
,求
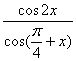的值。
19.已知函数y=sin2x－2cos2x＋3，求：①函数y的最大值及最大值时x的值；②函数y的增区间。
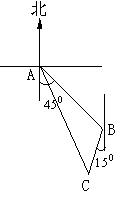
20．如图甲船在A处，乙船在A处的南偏东450方向B处，距A处有9海里并以20海里/小时的速度沿南偏西150方向行驶，若甲船以28海里/小时的速度行驶，应沿什么方向，用多少时间，才能追上乙船？
21．是否存在锐角，使得（1）
，（2）tan
tan=2-
同时成立？若存在求出的值，若不存在说明理由。