高一年级阶段考试数学试卷
注:考试时间100分钟,满分100分,请将答案写在答题纸上
一.选择题(本大题共10小题,每小题3分,计30分).
1.点P(1,-2)关于y轴对称的点的坐标是( )
A.(-1,-2) B.(1, 2) C.(-1,2) D.(-2,1)
2.如果全集![]() ,
,![]() ,
,![]() ,那么
,那么
(![]()
![]() )
)![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若ab=1,则![]() 的值为( )
的值为( )
A.1
B.-1 C.![]() D.2
D.2
4.若命题“p或q”是真命题,“非p”是假命题,那么( )
A.命题p一定是假命题 B.命题q一定是假命题
C.命题q一定是真命题 D.命题q是真命题或者是假命题

5.如图,□ABCD的周长为16cm,AC、BD
相交于点O,OE⊥AC交AD于E,则△DCE
的周长为( )
A.4 cm B.6cm
C.8cm D.10cm
6.若不等式![]() 的解集为
的解集为![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.有下列命题:①![]() 是错误的;②“
是错误的;②“![]() ”是“
”是“![]() ”成立的充分不必要条件;③“
”成立的充分不必要条件;③“![]() ”是“
”是“![]() 或
或![]() ”的充要条件;
”的充要条件;
④“菱形的两条对角线互相平分”的逆命题为真.其中正确的是( )
A.②④ B.② C.①③ D.②③
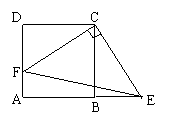 8.如图,正方形ABCD的面积为256,点F在
8.如图,正方形ABCD的面积为256,点F在
AD上,点E在AB的延长线上,RtΔCEF的
面积为200,则BE的长为( )
A.10 B.11
C.12 D.15
9.已知反比例函数![]() 的图象经过点
的图象经过点![]() ,则使得函数值
,则使得函数值![]() 的
的![]() 的取值集合为( )
的取值集合为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.设b>a,将一次函数y=bx+a与y=ax+b的图象画在平面直角坐标系内,则有一组a、b的取值,使得下列4个图中的一个为正确的是( )
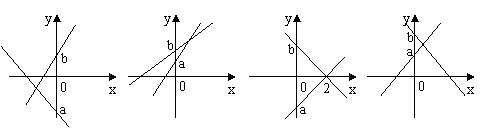
A B C D
二.填空题(本大题共4小题,每小题4分,计16分)
 11.满足
11.满足![]() 的集合共A有
个.
的集合共A有
个.
12.如图,在边长为4的正方形内部,以各边为直径画
四个半圆,则图中阴影部分的面积是 .
13.设集合![]() ,
,![]() ,
,
则集合{xx∈A且![]() =
.
=
.
14.一机器狗每秒钟前进或后退一步,程序设计师让机器狗以前进3步,然后再后退2步的规律移动.如果将此机器狗放在数轴的原点,面向正的方向,以1步的距离为1单位长.令P(n)表示第n秒时机器狗所在位置的坐标,且P(0)=0.现有如下判断:①P(3)=3;②P(5)=1;③P(10)=2;④P(101)=21;⑤P(103)<P(104),则所有正确判断的序号为 .
三.解答题(本大题共5小题,计54分)
15.(本小题满分10分)
解不等式:![]() .
.
16.(本小题满分10分)
已知集合![]() ,
,![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
17.(本小题满分10分)
如图,在直角坐标系xoy中,半径为2的⊙O与x轴交于A、B两点,与y轴交于点P,T是OB上一点,![]() ,过 A作AC⊥AB,且AC=AT,连结CP并延长交半圆于另一点Q,且Q恰为
弧PB的中点.
,过 A作AC⊥AB,且AC=AT,连结CP并延长交半圆于另一点Q,且Q恰为
弧PB的中点.
(1)求出点Q的坐标;
(2)求直线CP的解析式及![]() 的值;
的值;
 (3)由点P发出的光线,经过T点处反射后,反射光线是否通过点Q?请说明理由.
(3)由点P发出的光线,经过T点处反射后,反射光线是否通过点Q?请说明理由.
18.(本小题满分12分)
命题甲:方程![]() 有两相异负根;
有两相异负根;
命题乙:不等式![]() 对任意
对任意![]() 都成立.
都成立.
若这两个命题有且只有一个成立,求实数![]() 的取值范围.
的取值范围.
19.(本小题满分12分)
已知二次函数![]() ,其中
,其中![]() ,
,![]() ,且
,且![]() .
.
(1)用反证法证明:![]() ;
;
(2)求证:![]() ;
;
(3)求证:该函数图象与![]() 轴必有两个不同的交点A、B,并求线段AB长的取值范围.
轴必有两个不同的交点A、B,并求线段AB长的取值范围.
参 考 答 案
一.选择题(本大题共10小题,每小题3分,计30分).
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | D | A | D | C | A | B | C | B | B |
二.填空题(本大题共4小题,每小题4分,计16分)
11. 2 ; 12. 4 ;
13. {x1≤x≤3} ; 14. ①②③④ .
三.解答题(本大题共5小题,计54分)
15.解:![]() .(若有等于-1,扣2分)
.(若有等于-1,扣2分)
16.解:![]() ;(3分)
;(3分)
若![]() ,则
,则![]() ;
;
 若
若![]() ,则
,则![]() .(4分)
.(4分)
![]() ,
,![]() ,
,![]() .(3分)
.(3分)
![]() 17.(1)
17.(1)![]() ;(2分)
;(2分)
(2)![]() ;(2分)
;(2分)
![]() ;(2分)
;(2分)
(3)法一:![]() ,
,![]() ,
,
故反射光线通过点Q.(4分)
法二:如图,过Q点作QK垂直于x轴,垂足为K点,
可得![]() ,∴RtΔPOT∽RtΔQKT,
,∴RtΔPOT∽RtΔQKT,![]() 。
。
18.解:命题甲:![]() ,得
,得![]() ;
;
![]() ,得
,得![]() ,
,
![]() .(4分)
.(4分)
命题乙:若![]() ,得
,得![]() ,或
,或![]() (舍);
(舍);
若![]() ,则
,则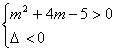 ,
,
解之得![]() ,
,![]() .(4分)
.(4分)
若甲成立乙不成立,则![]()
![]() ;
;
若甲不成立乙成立,则![]()
![]() ;
;
故m取值范围为![]() .(4分)
.(4分)
19.解:(1)设![]() ,则由
,则由![]() ,有
,有![]() ,
,
于是![]() ,与
,与![]() 矛盾,因此
矛盾,因此![]() .(2分)
.(2分)
(2)将![]() 代入
代入![]() 中即可证得.(4分)
中即可证得.(4分)
(3)可证得![]() ,
,![]() ,故图象与x轴有两不同交点。
,故图象与x轴有两不同交点。
![]() ,(4分)
,(4分)
![]() .(2分)
.(2分)