高一年级期末复习题
一、选择题（每题4分，共60分）
1、如果A = 
，那么错误的结论是
（ ）
A 0
B 
C 
D 
2、设甲、乙、丙是三个命题，如果甲是乙的必要条件，丙是乙的充分条件，但不是乙的必要条件，那么 （ ）
A 丙是甲的充分而不必要条件 B 丙是甲的必要而不充分条件
C 丙是甲的充要条件 D 丙既不是甲的充分条件也不是甲的必要条件
3、下列四组中的函数f (x)与g ( x ),表示相同函数的一组是 （ ）
A
f ( x ) = 
, g ( x ) =(
)
B f( x )= 
, g(x) =
C f ( x ) = x
,
g ( x ) =
D f ( x ) = x, g ( x ) =
4、已知函数f ( x ) = 
满足f(-1+x) = f (-1- x),且在闭区间
上的值域为
，则m的取值范
（ ）
A 
B 
C 
D 
5定义运算a☆b为：a☆b=
如1☆2 =1，则函数f( x )=
☆
的值域为
A、R B、
C、
D、 
6、函数y = -x(x≤0 )的反函数是
（
）
A y = - 
( x≧0 ) B y = 
( x≤0)
C y = - ( x≤0) D y = -
( x≤0)
7、0．3，log
0.3,2
这三个数之间的大小顺序是
（ ）
A 0．3<2 < log0.3 , B 0．3 < log0.3 < 2
C log0.3 < 0．3 < 2 ,
D log0.3 <2 < 0．3
8、若集合S = 
，T = 
，则S∩T是
（ ）
A、S B、T C、 
D、 有限集
9、已知y = 
,当其值域为
时，则x的取值范围是 （ ）
A、
B、
C、
D、
10、已知y = log
(2 – ax)在
上是减函数，则a的取值范 （ ）
A、 
B、 
C、 （ 0，2） D、 
11、函数f(x) = log
- 2 (x
1),则f
(x)的定义域是
（ ）
A、 R B、 
C、 
D、（0，1）
12已知数列1，0，1，0，…，则不是它的通项公式的
是 （ ）
A、 
B、
C、 
D、 
13、在 a与b(a
b)两数之间插入n个数使它们与a、 b组成等差数列，则此数列的公差为
（ ）
A、 
B、 
C、 
D、
14、数列
是等差数列的充要条件是
（
）
A、 S
B、
C、
（a
D、
（a
15、数列
，
的前n项和是 （
）
A、
B、
C、 
D、
二、填空题（每题4分，共40分）
16、若集合A=
，B=
，则A
B=
,A
B=
。
17、设函数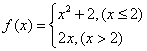
，则f(-4)= ,又知
则
18、有下列四个命题 ：
（1）函数y = 
在（0
）上不是增函数。（2）函数
在（-
，-1）
上是减函数，（3）函数
的单调增区间是
，（4）已知f(x)在R上是增函数，若a+b>0,则有f(a)+f(b) >f(-a)+f(-b),其中正确命题的序号是
。
19、已知函数y = f(x)是一次函数，且f(x)=1, 
,则f(x)的表达式为 。
20、将函数
的图象向右平移4个单位，再向上平移2个单位，可得到函数g(x)的图象，写出g(x)的解析式
。
21、方程
的解是
。
22、已知
，且f(lga)=100,则a = .
23、已知数列
则5
是它的第
项。
24、数列
的前n项和S
=2
，则
的值分别是 和 。
25、若a、b、 c成等比数列，则函数
的图象与x轴的交点个数为
。
三、解答题 （每题 10分，共50分）
26、已知集合A=
，B=
，且
，求p、q的值。
27、已知函数
，
（1） 求函数f(x)的定义域；
（2） 讨论函数f(x)的单调性；
（3）
解方程
；
28、已知
，且
。
（1）
求
的最小值及对应的x的值；
（2）
x为何值时，
且
。
29、已知满足
且
=1；
（1）
证明：数列
是等比数列；
（2）
求的表达式。
30、由分期付款方式购买家用电器一件价格为1150元，以后每月这一天都交付50元，并加付欠款的利息，月利率为1%，若交付150元以后的第一个月开始算分期付款的第一月，那么分期付款的第十个月应交付多少钱款？全部贷款付清后，买这件电器实际付了多少钱？
高一年级数学期末复习题答题卡
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| C | A | C | D | C | C | C | A | D | B | B | C | D | B | C |
二、填空题 ：
16、 B 、 A
。17、 18 、
。18、 （2）
。19、 f(x)=2x-1 。
20、
。21、 x=2 。 22、
23、 21 、
24、 3 、 18 。 25、 0 。
三、解答题：
26、解：
，则由题意可得：A=
，
P=-（-1+4）=-3
q=-1
4。
27、解：（1）要使f(x)
有意义，则
，当a>1时，
，当
时，
（2）当a>1时，定义域为
，任意
，且
，则
，
既：0<
,
,即当a>1时f(x)在上是增函数。同理可证：当0<a<1时f(x)在
上是增函数。
（3）由
或
（舍去）x = 
.
28解：（1）由
则
解得a=2或a=1(舍去)。
。
当
时，
最小，最小值为
。
（2）由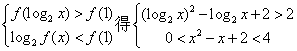
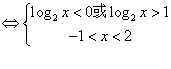
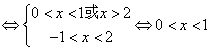
29、（1）证明：
，
是等比数列且q=2。
（2）
。
30解：购买时付了150元，欠款1000元，每月付50元，分20次付完，设每月付款数组，
则
。
依此类推，得，
。则是以
为首项，
为公差的等差数列。
（元）。
全部欠款付清后，一共支付钱款
（元）
答：分期付款的第十个月应交付55
5元，全部贷款付清后，买这件电器实际付了1255元。