第一章《集合与简单逻辑》基础测试题1

基础测试

（一）选择题（每小题5分，共30分）

1．下列各命题，正确的为（　　）．

（A）0　　（B）｛0｝　　（C） ＝｛0｝　　（D） ｛0｝

【提示】注意空集为任何非空集合的真子集．

【答案】（B）．

2．设A＝x｜x＜2，B＝x｜x²＜4，则下列各式正确的是（　　）．

（A）AB　　（B）AB　　（C）A＝B　　（C）BA

【提示】B＝x｜－2＜x＜2．

【答案】（B）．

3．若p：x＞1　q：x²＞1，则p 是q 的什么条件（　　）．

（A）充分非必要条件　　　　 （B）必要非充分条件

（C）充要条件　　　　　　　 （D）非充分也非必要条件

【提示】p q 但q　 q．

【答案】（A）．

4．下列各集合中，与集合｛x｜x²＝1，xR｝不相等的集合为（　　）．

（A）｛1，－1｝　　　　　　 （B）｛x｜x＝1，xR｝

（C）｛x｜x＝，xR｝　 （D）｛x｜x³＝x，xR｝

【提示】判断两个集合是否相等，关键是看它们所含的元素是否完全相同（注：两个相等的集合可以有不同的特征性质，但这些不同的性质所决定的元素必须是完全相同的）．（D）集合比其他四集合的元素多了一个0．

【答案】（D）．

5．满足｛a，b｝M｛a、b、c、d、e｝的集合M的个数是（　　）．

（A）2个　　（B）4个　　（C）7个　　（D）8个

【提示】本题主要考查子集与真子集的概念，由题意易知，集合M至少由｛a、b、c、d、e｝中的二个元素a、b 组成，但又不能同时有这5个元素．

【答案】（C）．

6．若关于x的一元二次不等式ax²＋bx＋c＜0的解集为实数集R，则a、b、c 应满足的条件为（　　）．

（A）a＞0，b²－4 ac＞0　　　（B）a＞0，b²－4 ac＜0

（C）a＜0，b²－4 ac＞0　　　（D）a＜0，b²－4 ac＜0

【提示】本题主要考查一元二次不等式与一元二次函数间的内在联系；“求不等式ax²＋bx＋c＜0的解集”等价于“当x为何值时，函数y＝ax²＋bx＋c 值小于0”．由题意知，y＝ax²＋bx＋c（a≠0）的图象开口向下，且与x轴无交点．

【答案】（D）．

（二）填空题（每小题5分，共30分）

1．已知A＝｛x｜x＞1｝，B＝｛x｜x²≤2｝，则AB＝_______________．

【提示】B＝｛x｜－≤x≤｝．

【答案】x｜1＜x≤

2．A＝｛x｜x＝2 n＋1，n Z｝，B＝｛x｜x＝4 n＋1，n Z｝则A_____B（填，，＝）．

【提示】A由所有奇数组成，B由所有被4除余1的数组成．

【答案】AB．

3．已知A＝x｜x²－2 x－8＜0，B＝x｜x－a＜0，AB＝f．则a 的范围是________．

【提示】A＝x｜－2＜x＜4，B＝x｜x＜a．

【答案】a≤－2．

4．若集合A＝｛a、b、c｝，则集合A的子集共有_______个．

【提示】注意不要漏掉f 与A．

【答案】8．

5．已知集合A有10个元素，集合B有8个元素，AB有4个元素，则集合AB有___________个元素．

【提示】n（AB）＝n（A）＋n（B）－n（AB）或用文氏图解．

【答案】14．

6．已知A＝x｜0＜x＜3，B＝｛x｜x≥a｝若AB，则a 的取值范围是_________．

【提示】将集合A、B在同一数轴上表示出来．

【答案】a≤0．

（三）解答题（每小题10分，共40分）

1．解不等式6 x²＜x＋2．

【解】将不等式转化为6 x²－x－2＞0

∵　方程6 x²－x－2＝0的两根为x₁＝－，x₂＝

∴　不等式6 x²－x－2＞0的解集为x｜x＜－或x＞．

【答案】原不等式的解集为x｜x＜－或x＞．

2．已知m＜0，求mx－2＜0的解集．

【解】mx－2＜0m＜0

mx＜2m＜0

m＜0

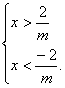
【答案】不等式mx－2＜0的解集为x｜＜x＜－．

3．已知集合A＝｛a²，a＋1，－3｝，B＝｛a－3，2 a－1，a²＋1｝，且AB＝｛－3｝，求实数a 的值．

【解】∵　AB＝｛－3｝

∴　－3B．

①若a－3＝－3，则a＝0，则A＝｛0，1，－3｝，B＝｛－3，－1，1｝

∴　AB＝｛－3，1｝与AB＝｛－3｝矛盾，所以a－3≠－3．

②若2 a－1＝－3，则a＝－1，则A＝｛1，0，－3｝，B＝｛－4，－3，2｝

此时AB＝｛－3｝符合题意，所以a＝－1．

4．用反证法证明：若a＞b＞0，则．

【证明】假设≤，

则≤0，

又≥0，

∴　（）（）≤0，

∴　a－b≤0．

∴　a≤b 这与已知a＞b 矛盾，所以假设不成立，即原命题为真．