第一章《集合与简单逻辑》提高测试题(二)1

提高测试（二）

（一）选择题（每小题5分，共30分）

1．若x²－2 x－3＜0则（　　）．

（A）x＜－1　　　　（B）x＞3

（C）x＞0　　　　  （D）x＜8

【提示】x²－2 x－3＜0－1＜x＜3x＜3

本题寻求的是x²－2x－3＜0的必要条件而不是充要条件．

【答案】（D）．

2．已知xR，y R^＋，集合A＝｛x²＋x＋1，－x，－x－1｝，

集合B＝｛－y，，y＋1｝，若A＝B，则x²＋y² 的值是（　　）．

（A）5　　（B）4　　（C）25　　（D）10

【提示】－x－1＜－x≤x²＋x＋1

∵　y R^＋，

∴　－y＜－＜y＋1．

∵　A＝B

∴　 

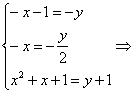
经检验，x＝1，y＝2满足集合元素的互异性，所以x²＋y²＝5．

【答案】（A）．

3．I为全集，集合A，B满足AB＝I，那么

①_IA_IB＝，②A∩_IB＝_IB，③A∪_IB＝A，④B_IA

四个命题中正确的命题的个数是（　　）．

（A）1　　（B）2　　（C）3　　（D）4

【提示】（1）_IA_IB＝ _I（AB）＝ _I I＝

（2）AB＝IA＝_IBA_IB＝_IB

（3）AB＝I_IB＝AA_IB＝A

（4）AB＝IB＝_IAB_IA

所以（1），（2），（3），（4）都正确．

【答案】（D）．

4．M＝｛x｜x＝3 m＋5 n，m，n Z｝，N＝｛x｜x＝2 m＋4 n，m、n Z｝那么M与N的关系是（　　）．

（A）M＝N　　（B）MN　　（C）MN　　（D）MN＝

【提示】略解1：集合M中同时含有奇数、偶数；集合N中仅含偶数，

所以（A）（B）一定是错误的，又因为8M，8N

∵　MN＝

∴　（D）错误．由排除法得答案为（C）．

略解2：对任意的x₀ N，则必存在着m₀，n₀ Z

若x₀＝2 m₀＋4 n₀＝3（－m₀－2 n₀）＋5（m₀＋2 n₀）

∵　－m₀－2 n₀ Z，m₀＋2 n₀ Z

∴　x₀ M

∴　NM．

又　3M，3N

∴　NM．

【答案】（C）．

5．关于x的二次方程x²＋（a²－1）x＋a－2＝0的一个根比1大，另一个根比1小的充要条件是（　　）．

（A）－1＜a＜1　　　 （B）a＜－1或a＞1

（C）－2＜a＜1　　　 （D）a＜－2或a＞1

【提示】略解1：设函数y＝x²＋（a²－1）x＋（a－2）

由图象易知：方程x²＋（a²－1）x＋a－2＝0的一个根比1大，一个根比1小

1＋（a²－1）＋a－2＜0 －2＜a＜1．

略解2：设方程的两个根为x₁、x₂，x₁＞1＞x₂

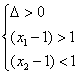
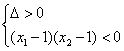
则－2＜a＜1．

【答案】（C）．

6．在坐标平面内，纵横坐标都是整数的点，叫做整点，我们用I表示所有直线的集合，M表示恰好通过一个整点的直线的集合，N表示不通过任何整点的直线的集合，P表示通过无穷整点的直线的集合，那么表达式正确的有几个（　　）．

（1）MNP＝I

（2）N≠

（3）M≠

（4）P≠

（A）1　　（B）2　　（C）3　　（D）4

【提示】构造出y＝x，y＝，y＝＋，y＝x来说明（2）、（3）、（4）均是正确的，所以本题的难点在于证明过两个整点的直线一定过无数个整点．设直线ax＋by＝G 过整点（x₀，y₀），（x₀，y₀）易证直线必过整点（（n＋1）x₀－x_0，（n＋1）y₀－y₀）所以直线ax＋by＝G 必过无数个整点．

【答案】（D）．

（二）填空题（每小题6分，共30分）

1．已知I＝R，集合A、B都是实数集I的子集．A_IB＝x｜x²＜4，A_IB＝｛x｜（x－4）（8－x）≥0｝，_IA_IB＝｛x｜x²－6 x－16＞0｝，求则AB＝____________．

【提示】

A_IB＝x｜x²＜4＝x｜－2＜x＜2，

_IAB＝｛x｜（x－4）（8－x）≥0｝＝｛x｜4≤x≤8｝，

_IA_IB＝｛x｜x²－8 x－16＞0｝＝x｜x＞8或x＜－2．

由文氏图易知AB＝（A_IB）（_IAB）（_IA_IB）

将A_IB，_IAB，_IA_IB分别画在同一条轴上．

【答案】AB＝x｜2＜x＜4．

【点评】本题涉及的各集合关系较多，采用文氏图和数轴表示使集合间的各种关系较为直观．其中AB＝（_IAB）（A_IB）（_IA_IB）这一关系式可由集合的基本运算推出．

2．集合M＝｛x｜x＝2ⁿ－2^k，n、k N且n＞k｝，集合P＝｛x｜1901≤x≤2000且xN｝则集合MP中所有元素的和为______________．

【提示】

∵　x≥1901

∴　2ⁿ＞1901

∴　n≥11．

当n＝12时，2ⁿ－2^k 的最小值为2¹²－2¹¹＝2048＞2000

∴　n＝11，进一步推理易知，k＝7或6，

∴　MP＝｛2¹¹，－2⁷，2¹¹，－2⁶｝＝｛1920，1984｝

∴　MP中各元素的和为 1920＋1984＝3904．

【答案】3904．

【点评】运用不等式控制的方法求出n的值是解题关键．

3．已知集合A＝｛（x，y）｜y＝ax＋2｝，B＝｛（x，y）｜y＝x＋1｝，且AB是一个单元集，则实数a 的取值范围为________________．

【提示】运用函数图象．

【答案】－∞，－11，＋∞．

4．已知集合A＝｛x｜x＝a²＋1，a N_＋｝，B＝｛y｜y＝b²－6 b＋10，b N_＋｝，则A与B的关系为________________．

【提示】B＝｛y｜y＝（b－3）²＋1，b N_＋｝，当b＝4，5，6，…时，y 的值与集合A中a＝1，2，…时，x的值相同，而b＝3时，y＝1B，但1A．

【答案】AB．

5．已知I＝｛（x，y）｜x，y R｝，A＝｛（x，y）｜y＝3 x－2｝，B＝｛（x，y）｜＝3｝，则_IAB＝____________．

【提示】B＝｛（x，y）｜y＝3 x－2，x≠2｝．

【答案】｛（x，y）｜x，yR且（x，y）≠（2，4）｝．

（三）解答题（第1，2小题每小题13分，第3小题14分，共40分）

1．已知集合M＝｛x｜x＝12 m＋8 n＋4 k，m、n、k Z｝与N＝｛x｜20 p＋16 q＋12 r，p、q、r Z｝，求证：M＝N．

【证明】

（1）证MN

对任意的x₀ M， 则必存在m₀、n₀、k₀ Z，使x₀＝12 m₀＋8 n₀＋4 k₀

＝20 n₀＋16 l₀＋12（m₀－n₀－k₀）

∵　n₀，k₀，m₀－n₀－k₀ Z

∴　x₀ N．

∴　MN．

（2）证NM

对任意的x₀ N，则必存在p₀、q₀、r₀，使x₀＝20 p₀＋16 q₀＋12 r₀＝12（r₀＋p₀＋q₀）＋8 p₀＋4 q₀．

∴　x₀ M．

∴　NM．

综上知，M＝N．

【点评】将系数为12，8，4的代数式与系数为20，16，12的代数式互相转化是解题的难点也是关键，为解决这个难点可采用待定系数法．

2．设M＝｛1，2，3，…，1995｝，A是M的子集，且满足条件：若kA时，则15k不属于A，求A中最多能有多少个元素？

【解】（1）构造125个数组：（9，9×15）；（10，10×15），…，（133，19×15）

由条件知A中不能同时包含任一数组中的两个数，所以A中元素的个数不会超过1995-125＝1870个

（2）当A＝｛1，2，…，8，134，135，…1995｝时满足条件，所以A中元素可达1870个

综合（1）（2）知，A中最多有1870个元素。

3．设A＝｛xy｜≤1｝，B_m＝｛x，y｜y＝－（x－m）²＋2 m｝，B＝，求AB的面积．

【解】集合A可以看作是以（0，1）为圆心，以1为半径的圆及圆内所有点的集合；

B_m表示以（m，2m）为顶点，形状与相同的抛物线；

B表示当m运动变化时，得到的所有B_m的并集，如图。

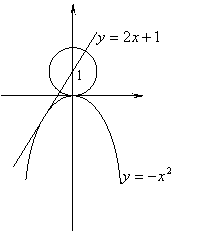当 变化时，B_m的顶点的轨迹为一条直线。

设直线与抛物线y＝－（x－m）²＋2 m相切

∴　＝－（x－m）²＋2 m

∴　Δ＝

即　

　　　　 k＝1

∴　B表示直线以下的部分（含上的点）

∵　点（0，1）在直线上

∴　AB即为半圆．

∴　AB的面积为．