第一章《集合与简单逻辑》提高测试题(一)1

提高测试（一）

（一）选择题（每小题5分，共30分）

1．已知I为全集，集合M，NI，若MN＝N，则（　　）．

（A）_I M_I N　　　　（B）M_I N

（C）_I M_I N　　　　（D）M_I N

【提示】本题涉及M、N、I、_IM、_IN五个集合之间的关系，若直接应用逻辑推理较为抽象，我们用文氏图表示出各集合的关系，答案一目了然．

【答案】（A）．

2．三个关于x的方程x²＋ax＋4＝0，x²＋（a－1）x＋16＝0，x²＋2 ax＋6 a＋16＝0至少有一个方程有实根，则实数a 的取值范围是（　　）．

（A）－4≤a≤4　　　　（B）－2＜a＜4

（C）a≤－2或a≥4　 （D）a＜0

【提示】“三个方程至少有一个方程有实数”等价于“三个判别式至少有一个大于等于0”所以本题是求集合｛a｜a²－16≥0｝；｛a｜（a－1）²－64≥0；｝；｛a｜4 a²－4（6 a＋16）≥0｝的并集，而不是交集，即不是解不等式组

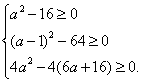
【答案】（C）．

3．条件甲：P Q＝P，条件乙：P Q，那么（　　）．

（A）甲是乙的充分而不必要条件

（B）甲是乙的必要而不充分条件

（C）甲是乙的充分且必要条件

（D）甲既不是乙的充分条件，也不是乙的必要条件．

【提示】由P Q＝P，则既可能P Q，也可能P＝Q，因而得不出甲乙，但由P Q，必有P Q＝P，因而乙甲．

【答案】（B）．

4．已知M＝｛x｜x＝a²＋b²，a、b 都为整数｝，N＝｛x｜x＝x₁·x₂，x₁，x₂ M｝．则下列正确的为（　　）．

（A）MN　　（B）MN　　（C）M＝N　　（D）MN＝

【提示】N＝｛x｜（a₁²＋b₁²）·（a₂²＋b₂²），a₁，b₁，a₂，b₂ Z｝

＝｛x｜（a₁a₂＋b₁b₂）²＋（a₁b₂－a₂b₁）²，（a₁a₂＋b₁b₂），（a₁b₂－a₂b₁）Z｝

【答案】（C）．

5．已知A＝｛（x，y）｜ax－y²＋b＝0｝，B＝｛（x，y）｜x²－ay－b＝0｝，（1，2）AB，则（　　）．

（A）a＝－3，b＝－7　　 （B）a＝3，b＝－7

（C）a＝－3，b＝7　　　 （D）a＝3，b＝7

【提示】（1，2）AB则（1，2）A且（1，2）B．

【答案】（C）．

6．已知A＝｛y｜y＝x²－2 x＋3，xR｝，B＝｛y｜y＝x－7，xR｝，则AB等于（　　）．

（A）｛（4，－3），（－1，－8）｝　 （B）｛y｜y≥2｝

（C）｛y｜y＝－3或－8｝　　　　（D）以上答案都不对

【提示】A＝｛y｜y≥2｝，B＝｛y｜y R｝＝R．

【答案】（B）．

（二）填空题（每小题5分，共30分）

1．已知x、y、z 为非零实数，用列举法将＋＋＋＋的所有可能值构成的集合表示出来为________________．

【提示】按x、y、z 的正、负分类讨论．

【答案】｛－3，－1，1，5｝．

2．1，2，…，1000中，既不是2的倍数，又不是5的倍数的数有__________个．

【提示】设A＝｛x｜x是2的倍数且1≤x≤1000｝，B＝｛x｜x是5的倍数且1≤x≤1000｝，I＝｛1，2，3，…，1000｝，则_IA_IB＝_I（A∩B）．

【答案】400．

3．集合M＝｛1，2，3｝的所有非空子集的元素和为_____________．

【提示】可先写出M的所有非空子集，再算元素和；也可先计算每个元素算了几遍．

【答案】24．

4．已知集合A＝｛x｜x²＋（p－2）x＋1＝0｝；AR_＋＝，则实数p 的取值范围是_________．

【提示】“AR_＋＝”“D＜0或x₁＜0，x₂＜0”所以本题是求集合p｜D＜0，p｜x₁＜0，x₂＜0的并集，其中p｜D＜0，p｜x₁＜0，x₂＜0＝｛p｜x₁＋x₂＜0，且x₁x₂＜0＝．

【答案】0＜p＜4．

5．若不等式x＋1≥kx对xR恒成立，则x的取值范围是______________．

【提示】将本题转化为函数问题解决，设y₁＝x＋1，y₂＝kx，易知y₁＝x＋1的图象为一条折线，y₂＝kx为过原点的直线．

【答案】0＜k＜1或k＞－1．

6．如果全集I＝｛x｜x为小于20的非负偶数｝，并且A∩_IB＝｛4，8，16｝，_IAB＝｛10，14，18｝，_IA_IB＝，则集合_IA_IB＝_____________．

【提示】将本题所涉及的集合用文氏图表示出来，则其中的关系会直观地显示出来．如图

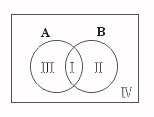
【答案】｛4，8，10，14，16，18｝．

（三）解答题（每小题10分，共40分）

1．已知A＝｛x｜x²－3 x＋2≤0｝，B＝｛x｜x²－（a＋1）x＋a≤0｝．

（1）若AB，求a 的取值范围；

（2）若BA，求a 的取值范围；

（3）若AB中只含有一个元素，求a 的数值．

【解】A＝｛x｜x²－3 x＋2≤0｝＝｛x｜1≤x≤2｝

B＝｛x｜x²－（a＋1）x＋a≤0｝＝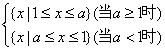

（1）∵　AB

∴　a≥1．

将A与B在同一数轴上表示出来，得：

∴　a＞2．

（2）∵　BA

∴　a≥1．

将A与B在同一数轴上表示为：

∴　1≤a＜2．

（3）∵　1A、1B，AB中只含一个元素

∴　AB＝｛1｝

∴　a≤1．

2．解不等式x－x－2＞1．

【解】x－x－2＞1

 或或

x≥2或＜x＜2或x

∴　不等式x－x－2＞1的解集为x｜x≥2或＜x＜2 ．

即 ｛x｜x＞｝．

3．用反证法证明：任意三角形中至少有一个角不大于60°．

【提示】已知△ABC 的三个内角分别为∠A、∠B、∠C．

求证：∠A、∠B、∠C 中至少有一个角不大于60°．

【证明】假设∠A、∠B、∠C 均大于60°

∴　∠A＋∠B＋∠C＞60°×3

即　∠A＋∠B＋∠C＞180°，这与三角形内角和为180°矛盾．

所以假设不成立，即原命题成立．

4．已知二次方程x²＋px＋q＝0有两个不等实根a、b，集合A＝｛1，3，5，7，9｝，B＝｛1，4，7，10｝，M＝｛a，b ｝，且MA＝，MB＝M，求p、q．

【提示】借助于文氏图表示集合A、B、M，如图．

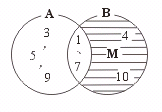
【答案】p＝－14，q＝40．