（二）B组
1. 已知I为全集，集合M，N
I，若M∩N=N，则（ ）。
（A）CIM
CIN
（B）MCIN
（C）CIM
CIN
（D）MCIN
答案：（A）
点评：本题涉及M、N、I、CIM、CIN五个集合之间的关系，若直接应用逻辑推理较为抽象，我们用维恩图表示出各集合的关系，答案就会一目了然。
2. 在三个关于x的方程x2+ax+4=0，x2+（a－1）x+16=0，x2+2ax+6a+16=0，至少有一个方程有实根，则实数a的取值范围是（ ）
（A）－4≤a≤4 （B）－2＜a＜4
（C）a≤－2或a≥4 （D）a＜0
答案：（C）
点评：“三个方程至少有一个方程有实根”等价于“三个判别式至少有一个大于等于0”所以本题是求集合{aa2－16≥0}；{a（a－1）2－64≥0；{a4a2－4（6a+16）≥0}的并集，而不是交集，即不是解不等式组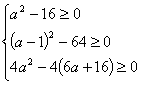
3. 条件甲：P∩Q=P，条件乙：PQ，那么（ ）
（A）甲是乙的充分而不必要条件
（B）甲是乙的必要而不充分条件
（C）甲是乙的充分且必要条件
（D）甲既不是乙的充分条件，也不是乙的必要条件。
答案：（B）
点评： 由P∩Q=P，则既可能PQ，也可能P=Q，因而得不出甲 乙，故甲不是乙的充分条件；但由PQ，必有P∩Q=P，因而乙 甲，故，甲是乙的必要条件。
4. 已知集合
；A∩R+=
，则实数P的取值范围是 。
答案：0＜P＜4
点评：“A∩R+=” “Δ＜0或x1＜0，x2＜0”所以本题是求集合
，
的并集，其中
，={Px1+x2＜0，且x1x2＜0}=Φ，所以答案为0＜P＜4
5. 若不等式x+1≥kx对x∈R恒成立，则x的取值范围是： 。
答案：0＜k＜1或k＞－1
点评：将本题转化为函数问题解决，共设y1=x+1，y2=kx，易知y1=x+1的图象为一条折线，y2=kx为过原点的一直
6. 如果全集I={xx为小于20的非负偶数}，并且A∩B={4，8，16}， A∩B={10，14，18}，A∩B =Φ，则集合 A∪B =
。
答案：{4，8，10，14，16，18}
评析：将本题所涉及的集合用维恩图表示出来，则其中的关系会直观地显示出来。如图：
Ⅰ表示A∩B，“Ⅰ+Ⅱ”表示B，“Ⅰ+Ⅲ”表示A。
Ⅱ为B∩A ，Ⅲ为A∩B，Ⅳ表示A∩B。
将各数填至相应部分即得答案。
7. 已知A={xx2－3x+2≤0}，B={xx2－（a+1）x+a≤0}。
1）若AB，求a的取值范围；
2）若BA，求a的取值范围；
3）若A∩B中反含有一个元素，求a的数值。
解：A={xx2－3x+2≤0}={x1≤x≤2}
B={xx2－(a+1)x+a≤0}= {x1≤x≤a}（当a≥1时）
{xa≤x≤1}（当a＜1时）
1）∵AB
∴易知a≥1
将A与B在同一数轴上表示出来得：
∴易知a＞2。
2）∵BA
∴易知a≥1
将A与B在同一数轴上表示为：
∴易知1≤a＜2。
3）∵1∈A、1∈B，A∩B中反含一个元素
∴A∩B={1}
∴a≤1。
点评：在处理集合之间的关系和集合的运算问题时，能将集合化简的要尽量化简，能用图形直观表示的要尽量采用，这样会使问题难度大大降低。
8. 解不等式x－x－2＞1
解：x－x－2＞1
或
或
X≥2或
或X∈
∴不等式X—X—2＞1的解集为{XX≥2或}
即{X X＞
}
点评：本题是将一个绝对值不等式的解集转化为三个一元一次不等式组解集的并集来解决的。
9、不等式a{x2+bx+c＞0}的解集是{X1＜X＜P}，求aX2+bx+a+0相解集
解：由已知有Q＜0，且2、B是方程ax2+b+x+c+0的两根
又2B=
，可推得C＜0。
又∵
，
是方程cx2+bx+a=0的两实根，且＞。
所以：cx2=bx+a+＜0的解集为{X1 X＜或X＞＝
点评：在解二次不等式cx2+bx+a＜0时，首先应判断二次项系数0＜的符号。即抛物线y=cx2+bx+a的开口方向，再判断方程cx2+bx+a=0的实根情况，若有实根，应求出它的实根，再根据图象开口方向和原不等式中不等号的方向及两实根的大小关系写出解集。本题中发现，是方程cx2+bx+a=0的两实根是解题关键之处。
10、用及证法证明：任意三角形中至少有一个角不大于60°
已知，△ABC的三个内角分别为∠A∠B∠C
求证：∠A∠B∠C中至少有一个角不大于60°
证明：假设∠A∠B∠C均大于60°
∴∠A∠B∠C＞60°×3
即∠A∠B∠C＞180°这与三角形内角和为180°矛盾
所以假设不成立，即原命题成立
点评：在用反证法证明命题时，最基础的一步是能正确地写出原命题的否命题。本题中原命题为“P或Q”形式的命题（即：∠A60°或∠B60°或∠C60°）在写这类命题的否命题时，应为“P且q”的形式（即∠A60°且∠B60°且∠C60°）在此转化过程中，相当于应用了德模根律：A∪BUC= A∩B∩ C。